三角比の2次関数の最大最小値を求めていきます。基本はほとんど2次関数の問題ですが、\(\sinθ\)や\(\cosθ\)の値の範囲に注意します。
(問題)
\(0°≦θ≦180°\) のとき、\(y=\sin^2θ-\cosθ\) の最大値と最小値、およびそのときの\(θ\)の値を求めよ。
(解答)
\(y=\sin^2θ-\cosθ=-\cos^2θ-\cosθ+1\)
\(\cosθ=t\) とおくと、\(0°≦θ≦180°\) のとき \(-1≦t≦1\)・・・①
\(y=-t^2-t+1=-(t+\displaystyle\frac{1}{2})^2+\displaystyle\frac{5}{4}\)・・・②
①の範囲で②のグラフを考えると
最大値 \(t=-\displaystyle\frac{1}{2}\) のとき \(\displaystyle\frac{5}{4}\)
最小値 \(t=1\) のとき \(-1\)
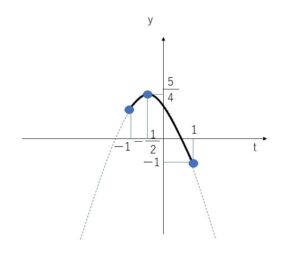
また、\(t=\cosθ=-\displaystyle\frac{1}{2}\) のとき \(θ=120°\)
\(t=\cosθ=1\) のとき \(θ=0°\)
したがって
最大値 \(\displaystyle\frac{5}{4}\) (\(θ=120°\))
最小値 \(-1\) \((θ=0°)\)
以上です。お疲れさまでした。
ここまで見て頂きありがとうございました。