(問題)
\(0°≦θ≦180°\) のとき、\(\cos^2θ+\sinθ+a=0\) が解をもつための\(a\)の値の範囲を求めよ。そのとき、解の個数を調べよ。
「方程式が解をもつ=方程式の\(y=\)(左辺) と \(y=\)(右辺) のグラフが共有点をもつ」 ことを利用します。定数\(a\)と変数\(θ\)(解答では\(\sinθ=t\)と置き換えている)を分離します。\(θ\)(解答では\(t\))のほうのグラフは横軸\(t\)、縦軸\(y\)の座標に固定して描くことができ、一方\(a\)のほうのグラフを動かすことで共有点をもつ場合を考えます。
念のため、上の「」内の性質の理由について。\(\cos^2θ+\sinθ+a=0\)では、変形すると、\(a=-\cos^2θ-\sinθ\)となるので、2つのグラフは\(y=a\) と \(y=f(θ)\) となります。この2つのグラフが共有点をもつということは、ある\(θ\)について2つのグラフの\(y\)座標が同じ値になるので、\(a=-\cos^2θ-\sinθ\)が成り立つ\(θ\)が存在することになります。
(解答)
与式より、\(1-\sin^2θ+\sinθ+a=0\)
整理すると、\(a=\sin^2θ-\sinθ-1\)
\(\sinθ=t\) とおくと、\(0°≦θ≦180°\) より \(0≦t≦1\)
また、方程式は \(a=t^2-t-1\)
与式より、\(1-\sin^2θ+\sinθ+a=0\)
整理すると、\(a=\sin^2θ-\sinθ-1\)
\(\sinθ=t\) とおくと、\(0°≦θ≦180°\) より \(0≦t≦1\)
また、方程式は \(a=t^2-t-1\)
ここで、\(y=a\)・・・① と \(y=t^2-t-1\) (\(0≦t≦1\))・・・②とおくと
\(y=t^2-t-1=(t-\displaystyle\frac{1}{2})^2-\displaystyle\frac{5}{4}\) から
②のグラフは図のようになる。
\(y=t^2-t-1=(t-\displaystyle\frac{1}{2})^2-\displaystyle\frac{5}{4}\) から
②のグラフは図のようになる。
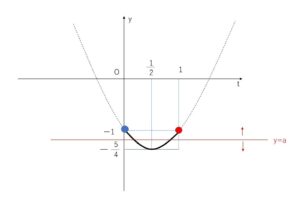
よって2つのグラフが共有点をもつときを考えると、方程式が解をもつ\(a\)の範囲は
\(-\displaystyle\frac{5}{4}≦a≦-1\)
(後半部分(解の個数)について)
\(t=\sinθ\)とおきかえたので単純に、「共有点の個数=解の個数」ではありません。例えば、\(a=-\displaystyle\frac{5}{4}\)のとき共有点は1つですが、その\(t\)座標は\(t=\displaystyle\frac{1}{2}\)で、\(t=\sinθ=\displaystyle\frac{1}{2}\)を満たす\(θ\)は、\(0°≦θ≦180°\) の範囲に2個(\(θ=30°,150°)\)存在するので、解の個数は2個です。共有点1つにつき\(θ\)が2個対応しているわけです。ただし、ある1点だけ共有点1個に対して\(θ\)が1個しか対応していない箇所があります。それは \(t=1\)です。(なぜなら、\(t=\sinθ=1\)を満たす\(θ\)は\(90°\)のみ)
解\(θ\)の個数は \(0°≦θ≦180°\) より、\(0≦t<1\)の範囲では \(t\) 1つに対して \(θ\) 2個、 \(t=1\) に対しては \(θ=90°\) の1個。
したがって
\(a=-\displaystyle\frac{5}{4}\) のとき 解は2個
\(-\displaystyle\frac{5}{4}<a<-1\) のとき 解は4個
\(-\displaystyle\frac{5}{4}<a<-1\) のとき 解は4個
\(a=-1\)のとき 解は3個
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
ここまで見て頂きありがとうございました。