・直線の傾きと\(tanθ\)の関係
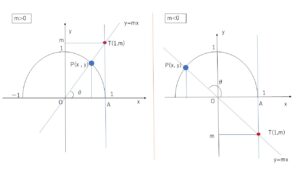
\(x\)軸の正の向きから左回りに原点を通る直線 \(y=mx\) まで測った角\(θ\)を、直線 \(y=mx\) と\(x\)軸のなす角といいます。なす角を\(θ\)とし、直線 \(y=mx\) と単位円の交点を\(P(x,y)\)とします。直線 \(y=mx\) は\(T(1,m)\)を通るので
\(\tanθ=\displaystyle\frac{y}{x}=\displaystyle\frac{m}{1}=m\)
となり、なす角\(θ\)の正接\(\tanθ\)は直線の傾き\(m\)と一致します。
また、直線 \(y=mx+n\) と\(x\)軸のなす角\(θ’\)は、この直線を原点を通るように平行移動した \(y=mx\) と\(x\)軸のなす角\(θ\)と等しいので以下のことが成り立ちます。
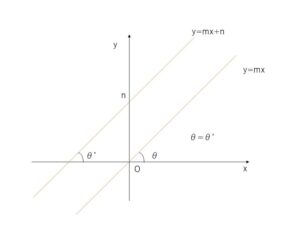
直線 \(y=mx+n\) と\(x\)軸のなす角が\(θ\)のとき
\(\tanθ=m\)
簡単にまとめると、\(\displaystyle\frac{y}{x}\)は、直線\(OP\)(直線\(OT\))の傾きそのものなので、
\(\displaystyle\frac{y}{x}=\tanθ=m\)となります。
\(\displaystyle\frac{y}{x}=\tanθ=m\)となります。
(例題)
次の2直線のなす鋭角\(θ\)を求めよ。
\(\sqrt{3}x-y-2=0\), \(x-\sqrt{3}y+1=0\)
2直線のなす角は、大きい方の角と小さい方の角の2つ(もしくは2つとも90°)が考えられます。どちらを答えにするかは問題文に従ってください。
(解答)
\(\sqrt{3}x-y-2=0\) より \(y=\sqrt{3}x-2\)・・・①
\(x-\sqrt{3}y+1=0\) より \(y=\displaystyle\frac{1}{\sqrt{3}}x+\displaystyle\frac{1}{\sqrt{3}}\)・・・②
\(\sqrt{3}x-y-2=0\) より \(y=\sqrt{3}x-2\)・・・①
\(x-\sqrt{3}y+1=0\) より \(y=\displaystyle\frac{1}{\sqrt{3}}x+\displaystyle\frac{1}{\sqrt{3}}\)・・・②
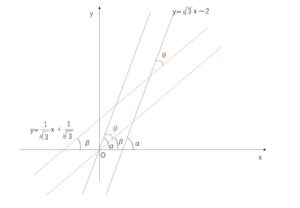
①と\(x\)軸のなす角を\(α\)、②と\(x\)軸のなす角を\(β\) (\(0°<α<180°\),\(0°<β<180°\)) とすると
\(\tanα=\sqrt{3}\) \(\tanβ=\displaystyle\frac{1}{\sqrt{3}}\)
よって、\(α=60°\) \(β=30°\)
\(\tanα=\sqrt{3}\) \(\tanβ=\displaystyle\frac{1}{\sqrt{3}}\)
よって、\(α=60°\) \(β=30°\)
したがって、\(θ=60°-30°=\)\(30°\)
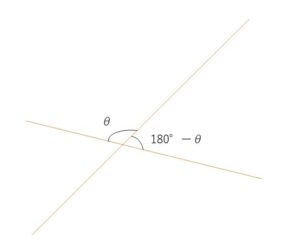
計算で出てきた角度が\(90°\)を超えるときは、\(180°\)からその角度を引いたものが答えになります。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。