今回は正弦定理について見ていきます。名前の通り\(\sin\)が登場する定理です。
・三角形と外接円
正弦定理を導く前に、まず三角形の辺と角に名前をつけます。
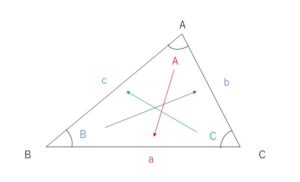
\(△ABC\)において、辺\(BC,CA,AB\)の長さをそれぞれ\(a,b,c\)とし、\(\angle A,\angle B,\angle C\)の大きさをそれぞれ\(A,B,C\)とします。
辺は角に向かい合う辺(対辺)をその角の小文字の記号で表します。例えば、\(\angle A\)の対辺\(BC\)は\(a\)です。
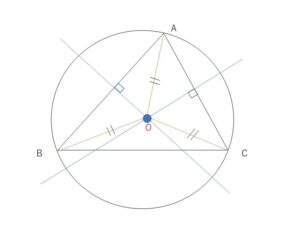
\(△ABC\)において、\(AB\)の垂直二等分線と、\(AC\)の垂直二等分線の交点を\(O\)とします。\(OA=OB\)かつ\(OA=OC\)なので、\(OA=OB=OC\)。よって\(O\)は3点\(A,B,C\)から等距離にある点なので、\(O\)を中心とする\(A,B,C\)を通る円が存在することになります。
\(△ABC\)について次の定理(正弦定理)が成り立ちます。
\(△ABC\)の外接円の半径を\(R\)とすると
\(\displaystyle\frac{a}{\sin A}=\displaystyle\frac{b}{\sin B}=\displaystyle\frac{c}{\sin C}=2R\)
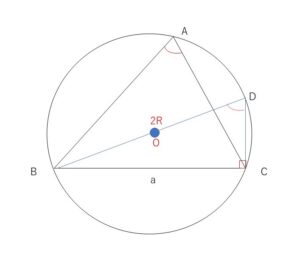
\(B\)を通る直径を\(BD\)とすると、円周角の定理より、\(A=D\)
直角三角形\(BCD\)について、\(\sin D=\displaystyle\frac{a}{2R}\)
\(\sin A=\displaystyle\frac{a}{2R}\)・・・(1)
\(A≠0°\) より \(\sin A≠0\) だから (1)を変形して
\(a=2R\) で \(\sin A=1\)だから
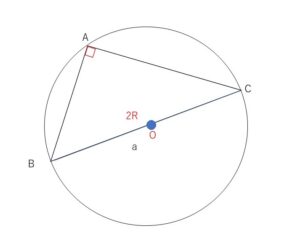
③\(A>90°\) のとき
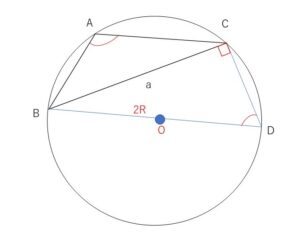
\(B\)を通る直径を\(BD\)とすると、四角形\(ABCD\)は円に内接しているので
\(A=180°-D\) 。よって \(\sin A=\sin(180°-D)=\sin D\)
また、直角三角形\(BCD\)において、\(\sin D=\displaystyle\frac{a}{2R}\)
しがって \(\sin A=\displaystyle\frac{a}{2R}\)・・・(2)
\(A≠180°\)より\(\sin A≠0\) だから (2)を変形して
\(\displaystyle\frac{a}{\sin A}=2R\)
以上①~③より、\(\displaystyle\frac{a}{\sin A}=2R\) が成り立つ。
また、同様にして、\(\displaystyle\frac{b}{\sin B}=2R\), \(\displaystyle\frac{c}{\sin C}=2R\) も成り立つので
\(\displaystyle\frac{a}{\sin A}=\displaystyle\frac{b}{\sin B}=\displaystyle\frac{c}{\sin C}=2R\)
\(a:b:c=\sin A:\sin B:\sin C\) となり、3辺の長さの比と正弦の値の比は一致します。
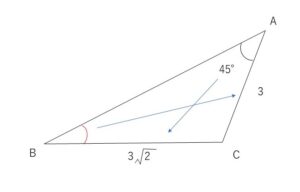
\(△ABC\)において、\(a=3\sqrt{2},b=3,A=45°\) のとき、\(B\)を求めよ。
正弦定理より
\(\displaystyle\frac{3\sqrt{2}}{\sin45°}=\displaystyle\frac{3}{\sin B}\)
よって、\(\sin B=\displaystyle\frac{1}{2}\)
よって、\(B=30°\)
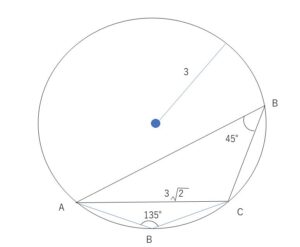
\(△ABC\)において、外接円の半径が\(3\)で\(b=3\sqrt{2}\)のとき、\(B\)の値を求めよ。
正弦定理より
\(\displaystyle\frac{3\sqrt{2}}{\sin B}=2・3\)
よって、\(\sin B=\displaystyle\frac{1}{\sqrt{2}}\)から
\(B=45°,135°\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。