三角形の角の二等分線に関する問題を見ていきます。問題を解く前に先に内角の二等分線に関するとても大事な定理を紹介します。
\(△ABC\)において、\(\angle A\)の二等分線と\(BC\)の交点を\(D\)とすると
\(AB:AC=BD:DC\)
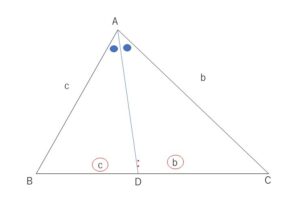
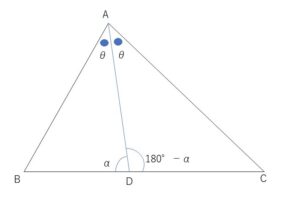
図のように、角\(θ,α\)を設定する。
\(△ABD\)において、正弦定理より
\(\displaystyle\frac{AB}{\sinα}=\displaystyle\frac{BD}{\sinθ}\)
よって、\(AB=BD\displaystyle\frac{\sinα}{\sinθ}\)・・・①
\(\displaystyle\frac{AC}{\sin(180°-α)}=\displaystyle\frac{DC}{\sinθ}\)
\(AC=DC\displaystyle\frac{\sinα}{\sinθ}\)・・・②
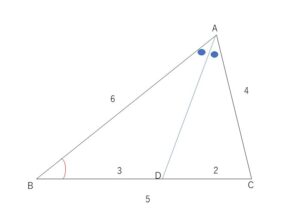
(問題)
\(AB=6,BC=5,CA=4\)である\(△ABC\)において、\(\angle A\)の二等分線と辺\(BC\)の交点を\(D\)とするとき、\(AD\)の長さを求めよ。
(解答)
\(AD\)は\(\angle A\)の二等分線だから
\(BD:DC=6:4=3:2\)
\(BC=5\) だから \(BD=5×\displaystyle\frac{3}{3+2}=3\)
\(△ABD\)において、余弦定理を用いると
\(AD^2=36+9-2・6・3\cos B\)・・・①
また、\(△ABC\)において余弦定理より
\(\cos B=\displaystyle\frac{36+25-16}{2・6・5}=\displaystyle\frac{3}{4}\)
①に代入して整理すると
\(AD^2=18\)
\(AD>0\) だから \(AD=3\sqrt{2}\)
※参考までに、角の二等分線の比の定理を知らない場合でもこの問題は解くことができます。(結構大変ですが)
(別解)
図のように角\(θ\)と辺の長さ\(AD=x,DC=a\)を設定する。
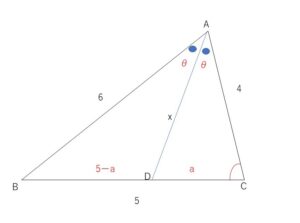
\(△ABD\)において余弦定理より
\(\cosθ=\displaystyle\frac{36+x^2-(5-a)^2}{2・6・x}\)・・・①
\(△ADC\)において余弦定理より
\(\cosθ=\displaystyle\frac{16+x^2-a^2}{2・4・x}\)・・・②
①②から\(\cosθ\)を消去して整理すると
\(x^2-a^2-20a+26=0\)・・・③
また、\(△ABC\)において余弦定理より
\(\cos C=\displaystyle\frac{16+25-36}{2・4・5}=\displaystyle\frac{1}{8}\)・・・④
\(△ADC\)において余弦定理より
\(\cos C=\displaystyle\frac{16+a^2-x^2}{2・4・a}\)・・・⑤
④⑤より \(\cos C\)を消去して整理すると
\(x^2-a^2+a-16=0\)・・・⑥
③-⑥より
\(-21a+42=0\) よって \(a=2\)
\(a=2\)を⑥に代入して
\(x^2=18\) \(x>0\)だから \(x=AD=3\sqrt{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
→高校数学TOP next→三角形の成立条件と辺と角の大小関係 back→正弦・余弦定理と比例式