三角形の角と三角比の大小

三角比の大小と角の大小の対応について見ていきます。(前回(3-6)の 辺と角の大小関係① でも少しだけ触れました。)

(問題)
\(△ABC\)において、\(BC>CA>AB\)である。\(\cos A \sin C\), \(\cos B\sin B\), \(\cos C\sin A\)　の中で最大なものを\(M\),最小のものを\(m\)とする。\(M,m\)を求めよ。

\(BC>CA>AB\) から角の大小は\(A>B>C\)で、\(A,B,C\)はすべて\(0°\)より大きく\(180°\)より小さい値です。\(\cosθ\)については、\(θ\)を\(0°→180°\)と変化させると、\(1\)から単調に減少して\(-1\)となるので、角が小さいほど三角比の値は大きくなるので、角と三角比の大小が入れ替わることに注意する以外は分かりやすいです。
しかし、\(\sinθ\)は、\(θ\)を\(0°→180°\)と変化させると、\(0\)から増加して、\(90°\)のとき最大値\(1\)をとり、\(90°\)を超えると今度は減少して\(0\)となるので、単純に角の大小と三角比の大小を対応させることができません。ただ、\(0°→90°\)のときは単調に増加する(\(90°→180°\)は単調に減少する)ことから、最大角\(A\)を\(90°\)を境目に場合分けしてやればうまく解けそうです。

(解答)
\(BC>CA>AB\) より　\(A>B>C\)

(1)\(90°>A>B>C\) のとき
余弦の値は角度が大きいほど小さいので
\(0<\cos A<\cos B<\cos C\)
正弦の値は角度が大きいほど大きいので
\(0<\sin C<\sin B<\sin A\)
よって、　\(0<\cos A \sin C<\cos B\sin B<\cos C\sin A\)

(2)\(180°>A≧90°>B>C\) のとき
余弦の値は角度が大きいほど小さいので
\(\cos A≦0<\cos B<\cos C\)・・・①

\(90°>B>C\)なので、
\(0<\sin C<\sin B\)・・・②

また、\(B+C=180°-A\)で
\(0°<B<B+C≦90°\)だから
\(0<\sin B<\sin(B+C)=\sin(180°-A)=\sin A\)
よって、\(\sin B<\sin A\)・・・③
②③より　\(0<\sin C<\sin B<\sin A\)・・・④

したがって①④より　\(\cos A \sin C≦0<\cos B\sin B<\cos C\sin A\)

以上(1)(2)より　\(M=\cos C\sin A\),　\(b=\cos A \sin C\)

\(0<a<b\)かつ\(0<x<y\) ならば　\(0<ax<ay\)　という性質を使いました。(2)の一番左の辺については\(a≦0\) かつ\(0<x\)ならば、\(ax≦0\)となるのはよいでしょう。

(2)の\(B<B+C\)という変形については、単位円と\(A,B,C\)の関係を図にすると思いつきやすいです。\(A≧90°\)、\(B+C≦90°\)、\(A+B+C=180°\)に注意して図を描くと次のとおり。

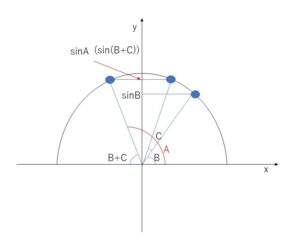
\(\sin(B+C)\) と \(\sin A\)が同じになることに気づくことがポイントです。

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→三角比の等式の証明　 back→三角形の成立条件と辺と角の大小関係