四角形の面積を求めるには、基本的には三角形に分割してそれぞれの三角形の面積の和を求めます。
(例題1)
平行四辺形\(ABCD\)において、\(AB=3,AC=5,AD=7\) のとき、平行四辺形の面積\(S\)を求めよ。
(解答)
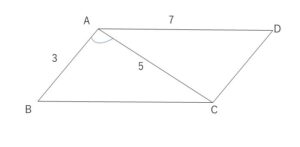
\(BC=7\) だから、\(△ABC\)で余弦定理より
\(\cos\angle BAC=\displaystyle\frac{3^2+5^2-7^2}{2・3・5}=-\displaystyle\frac{1}{2}\)
\(0°<\angle BAC<180°\) だから、\(\angle BAC=120°\)
したがって
\(S=2×\displaystyle\frac{1}{2}・3・5・\sin120°=\)\(\displaystyle\frac{15\sqrt{3}}{2}\)
(例題2)
\(AD/\!/BC\) の台形\(ABCD\)で,\(AB=5,BC=8,BD=7,\angle A=120°\) であるとき、この台形\(ABCD\)の面積\(S\)を求めよ。
(解答)
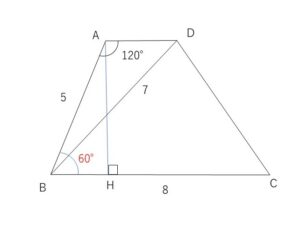
\(△ABD\)において余弦定理より
\(7^2=AD^2+5^2-2・AD・5・\cos120°\)
整理すると
\(AD^2+5AD-24=0\) \((AD+8)(AD-3)=0\)
\(AD>0\) だから \(AD=3\)
また、\(AD/\!/BC\) より \(\angle ABC=60°\) となり
\(A\)から\(BC\)に下した垂線の足を\(H\)とすると
\(AH=5・\sin60°=\displaystyle\frac{5\sqrt{3}}{2}\)
したがって
\(S=(3+8)・\displaystyle\frac{5\sqrt{3}}{2}×\displaystyle\frac{1}{2}=\)\(\displaystyle\frac{55\sqrt{3}}{4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。