今回からは立体図形です。平面図形より難易度は上がりますが、立体から平面図形を取り出すことが基本となります。
(問題)
1辺の長さが\(1\)である正四面体がある。
(1)この正四面体の高さを求めよ。
(2)この正四面体の体積を求めよ。
正四面体は4面がすべて正三角形です。この正四面体を\(ABCD\)とし、\(A\)から三角形\(BCD\)に下ろした垂線を\(AH\)とすると、\(AH\)が四面体の高さになります。また、\(△ABH,△ACH,△ADH\)はすべて斜辺が\(1\)の直角三角形で、\(AH\)が共通であるから合同です。したがって\(BH,CH,DH\)はすべて同じ長さとなり、\(H\)は\(△BCD\)の外心となります。外接円の半径を求めれば、あとは例えば\(△ABH\)で三平方の定理を用いれば、高さ\(AH\)が求まります。
(解答)
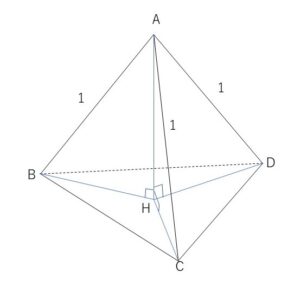

正四面体の頂点を\(ABCD\)とし、\(A\)から\(△BCD\)に垂線\(AH\)を下す。
\(△ABH≡△ACH≡△ADH\) であるから \(BH=CH=DH\)
よって、\(H\)は\(△BCD\)の外接円の中心だから、外接円の半径を\(R\)とすると正弦定理より
\(\displaystyle\frac{1}{\sin60°}=2R\)
よって \(R=BH=\displaystyle\frac{1}{\sqrt{3}}\)
\(△ABH≡△ACH≡△ADH\) であるから \(BH=CH=DH\)
よって、\(H\)は\(△BCD\)の外接円の中心だから、外接円の半径を\(R\)とすると正弦定理より
\(\displaystyle\frac{1}{\sin60°}=2R\)
よって \(R=BH=\displaystyle\frac{1}{\sqrt{3}}\)
また、\(△ABH\)で三平方の定理より
\(AH=\sqrt{AB^2-BH^2}=\sqrt{1-\displaystyle\frac{1}{3}}=\)\(\displaystyle\frac{\sqrt{6}}{3}\)
\(AH=\sqrt{AB^2-BH^2}=\sqrt{1-\displaystyle\frac{1}{3}}=\)\(\displaystyle\frac{\sqrt{6}}{3}\)
正三角形の 外心・内心・重心・垂心 はすべて一致します。なので重心の性質「重心は\(B\)から\(CD\)の中点を結ぶ線分を\(2:1\)に内分する」を利用しても\(BH\)は求まります。
(2)
四面体(三角錐)の体積\(=\displaystyle\frac{1}{3}\)×(底面積)×(高さ) です。
\(△BCD=\displaystyle\frac{1}{2}・1・1・\sin60°=\displaystyle\frac{\sqrt{3}}{4}\)
よって求める体積\(V\)は
\(V=\displaystyle\frac{1}{3}・\displaystyle\frac{\sqrt{3}}{4}・\displaystyle\frac{\sqrt{6}}{3}=\)\(\displaystyle\frac{\sqrt{2}}{12}\)
\(V=\displaystyle\frac{1}{3}・\displaystyle\frac{\sqrt{3}}{4}・\displaystyle\frac{\sqrt{6}}{3}=\)\(\displaystyle\frac{\sqrt{2}}{12}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。