正四面体に外接・内接する球について考えていきます。
(問題)
1辺の長さが\(a\)である正四面体\(ABCD\)について
(1)四面体に外接する球の半径\(R\)を求めよ。
(2)四面体の体積\(V\)を求めよ。
(3)四面体に内接する球の半径\(r\)を求めよ。
(解答)
(1)
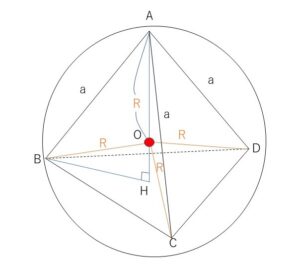
\(△BCD\)の外接円の半径を\(k\)とすると正弦定理により
\(2k=\displaystyle\frac{a}{\sin60°}\) だから
\(k=BH=\displaystyle\frac{a}{\sqrt{3}}\)
また、\(△ABH\)において三平方の定理より
\(AH=\sqrt{AB^2-BH^2}=\sqrt{a^2-(\displaystyle\frac{a}{\sqrt{3}})^2}=\displaystyle\frac{\sqrt{6}}{3}a\)
さらに、\(△OBH\)において三平方の定理より
\(OB^2=BH^2+OH^2\)で
\(OH=AH-AO=\displaystyle\frac{\sqrt{6}}{3}a-R\) だから
\(R^2=(\displaystyle\frac{a}{\sqrt{3}})^2+(\displaystyle\frac{\sqrt{6}}{3}a-R)^2\)
これを\(R\)について解くと
\(\displaystyle\frac{2\sqrt{6}}{3}aR=a^2\) で\(a≠0\)だから
\(R=\displaystyle\frac{\sqrt{6}}{4}a\)
(2)
\(△BCD=\displaystyle\frac{1}{2}a・a・\sin60°\) だから\(V=\displaystyle\frac{1}{3}・△BCD・AH\)
\(=\displaystyle\frac{1}{3}・\displaystyle\frac{\sqrt{3}}{4}a^2・\displaystyle\frac{\sqrt{6}}{3}a\)
\(=\displaystyle\frac{\sqrt{2}}{12}a^3\)
(3)
(2)で正四面体の体積を求めたのでこれを利用してみます。内接球の中心を\(I\)とすると、\(I\)と底面\(△BCD\)と内接球の接点\(T\)を結ぶと、\(IT\)と平面\(BCD\)は垂直に交わります。ここで四面体\(IBCD\)を考えてやると、これは底面\(BCD\)、高さ\(IH=\)内接球の半径\(r\) の四面体です。他の側面3つも全く同じように考えると、合計同じ体積の四面体が4つできます。これら4つの四面体の体積の和が全体の四面体\(ABCD\)の和であることを利用します。
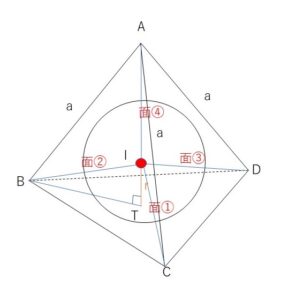
側面(図の面②~④)も同様に考えると、面②~④を底面として高さ\(r\)の四面体ができ、初めに考えたものを含め合計4つの同じ体積の四面体ができる。
\(\displaystyle\frac{\sqrt{2}}{12}a^3=4×(I-BCD\)の体積\()\)
\(\displaystyle\frac{\sqrt{2}}{12}a^3=4×(\displaystyle\frac{1}{3}・\displaystyle\frac{\sqrt{3}}{4}a^2・r)\)
なので体積の和を使わず、(1)で図形的に\(OH\)を求めても内接球の半径は求まります。
あえて球の中心\((O,I)\)と垂線の足\((H,T)\)と別の記号で書きましたが、結局は同じ点です。
※結構ハードな内容でしたね。何度か繰り返し練習すれば慣れますので頑張りましょう。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。