三角関数の定義

三角関数の定義について見ていきます。定義の仕方は三角比のところでやった円による定義と同様です。

 

・三角関数の定義
三角比の分野では\(0°≦θ≦180°\)の範囲において、座標平面上の円を用いて三角比を定義しましたが、一般角についても同様に定義します。

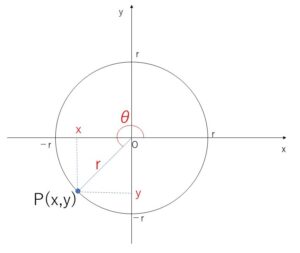
座標平面上で\(x\)軸の正の部分を始線にとり、角\(θ\)の表す動径と原点を中心とし半径\(r\)の円との交点\(P\)の座標を\((x,y)\)とし、角\(θ\)の正弦・余弦・正接を次のように定義します。

\(\sinθ=\displaystyle\frac{y}{r}\)　\(\cosθ=\displaystyle\frac{x}{r}\)　\(\tanθ=\displaystyle\frac{y}{x}\)

(ただし \(\tanθ\) については分母\(x\)が\(0\)になるとき、つまり \(θ=\displaystyle\frac{π}{2}+nπ\) (\(n\)は整数) のときは定義しません。)

 

ここで、円を拡大して半径\(kr\)の円について同じことを考えてみると、動径と円との交点を\(P’\)の座標は\((kx,ky)\)。よって　\(\sinθ\),\(\cosθ\),\(\tanθ\)　を計算すると

\(\sinθ=\displaystyle\frac{ky}{kr}\)\(=\displaystyle\frac{y}{r}\)
\(\cosθ=\displaystyle\frac{kx}{kr}\)\(=\displaystyle\frac{x}{r}\)
\(\tanθ=\displaystyle\frac{ky}{kx}\)\(=\displaystyle\frac{y}{x}\)

であり、半径\(r\)の場合と同じとなり半径を変化させても \(\displaystyle\frac{y}{r}\),\(\displaystyle\frac{x}{r}\),\(\displaystyle\frac{y}{x}\)の値は変わりません。また\(P\)の座標\(x,y\)は\(θ\)によって定まるので、\(\sinθ\),\(\cosθ\),\(\tanθ\)は角\(θ\)だけによって定まる\(θ\)の関数となり、これらの関数を三角関数とよびます。

 

・三角関数の値域
三角関数の値は半径の大きさに関係なく定まるので、分かりやすいように半径\(1\)の円(単位円)について考えることが多いです。

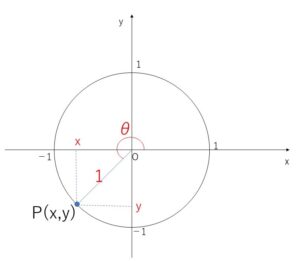
単位円と角\(θ\)の動径の交点を\(P(x,y)\)とすると

\(\sinθ=\displaystyle\frac{y}{1}=y\),　\(\cosθ=\displaystyle\frac{x}{1}=x\)

であり、点\(P\)は単位円上を動くので\(y,x\)は次の範囲を動きます。
\(-1≦y≦1\), \(-1≦x≦1\)

よって\(\sinθ\),\(\cosθ\)の値域は
\(-1≦\sinθ≦1\), \(-1≦\cosθ≦1\)

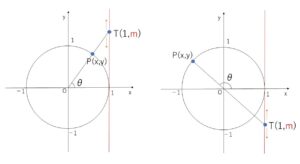
また \(\tanθ=\displaystyle\frac{y}{x}\) は直線\(OP\)の傾きを表し、\(\tanθ=m\)(傾き) とおくと、直線\(OP\)と直線\(x=1\)の交点\(T\)の座標は\((1,m)\)となります。

\(θ\)を変化させると、\(T\)は\(x=1\)上をどこでも動き得るので、\(T\)の\(y\)座標\(m\)つまり\(\tanθ\)はすべての実数値をとることになります。

 

・三角関数の値の符号
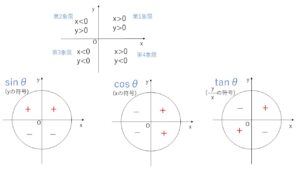
角\(θ\)の動径がどの象限にあるかによって円上の点\(P\)の座標\(x,y\)の符号が定まるので、角\(θ\)がどの象限にあるかによって三角関数の値の符号が決まります。
単位円で考えると \(\sinθ=y\)　\(\cosθ=x\)　\(\tanθ=\displaystyle\frac{y}{x}\) なので、それぞれ\(x,y,\displaystyle\frac{y}{x}\) の符号を考えることになります。
例えば第2象限にある場合は\(x<0\),\(y>0\)なので、\(\sinθ>0\), \(\cosθ<0\),　\(\tanθ<0\) です。まとめると以下の図の通りです。

 

 

(例題)次の三角関数の値を求めよ。
(1)\(\sin\displaystyle\frac{4}{3}π\)
(2)\(\cos(-30°)\)
(3)\(\tan(-\displaystyle\frac{13}{4}π)\)

 

 

(解答)
(1)

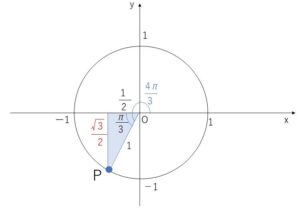
図より点\(P\)の\(y\)座標は \(-\displaystyle\frac{\sqrt{3}}{2}\)
よって \(\sin\displaystyle\frac{4}{3}π\)\(=\)\(-\displaystyle\frac{\sqrt{3}}{2}\)

(2)

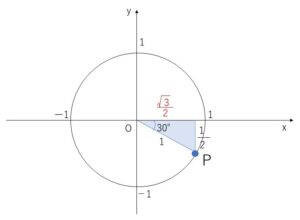
図より点\(P\)の\(x\)座標は \(\displaystyle\frac{\sqrt{3}}{2}\)
よって \(\cos(-30°)=\)\(\displaystyle\frac{\sqrt{3}}{2}\)

(3)

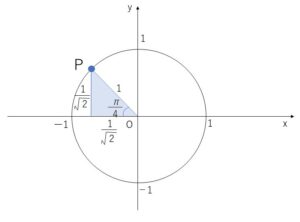
\(-\displaystyle\frac{13}{4}π=\displaystyle\frac{3}{4}π+2π×(-2)\)
図より直線\(OP\)の傾きは \(-1\) だから
\(\tan(-\displaystyle\frac{13}{4}π)=\)\(-1\)

 

 

 

 

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角関数の相互関係①　back→弧度法とその利用