三角関数のグラフの形状や特徴について見ていきます。
・三角関数のグラフ
まずは \(y=\sinθ\) , \(y=\cosθ\) について
①グラフの形状
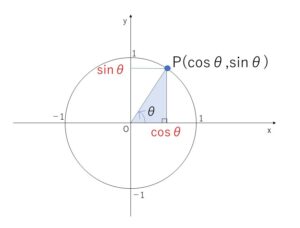
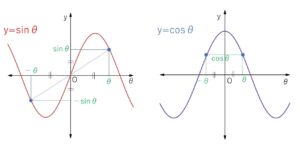
角\(θ\)の動径と単位円の交点を\(P\)とすると、\(P(\cosθ,\sinθ)\)となります。
つまり\(P\)の\(y\)座標が\(\sinθ\)、\(x\)座標が\(\cosθ\)なので、これを利用してグラフを次のように書くことできます。
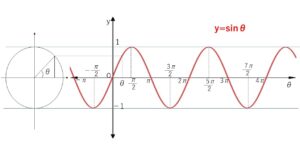
①\(θ\)が\(0→\displaystyle\frac{π}{2}\) のとき、\(y\)座標が\(0\)→\(1\)に上がり続ける
②\(θ\)が\(\displaystyle\frac{π}{2}→\displaystyle\frac{3}{2}π\) のとき、\(y\)座標が\(1\)→\(-1\)に下がり続ける
③\(θ\)が\(\displaystyle\frac{3}{2}π→2π\) のとき、\(y\)座標が\(-1\)→\(0\)に上がり続ける
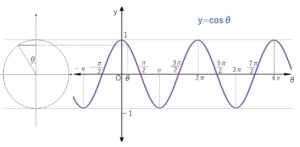
今回も同様に\(P\)の動きを考えると
①\(θ\)が\(0→π\)のとき、\(1→-1\)と下がり続ける
②\(θ\)は\(π→2π\)のとき、\(-1→1\)と上がり続ける
\(y=\sinθ\), \(y=\cosθ\) のどちらも値域は、\(-1≦y≦1\) となります。
またグラフからも、\(\sin(θ+\displaystyle\frac{π}{2})=\cosθ\) からも分かりますが、\(y=\sinθ\)のグラフを\(θ\)方向に\(-\displaystyle\frac{π}{2}\)平行移動すると、\(\cosθ\)のグラフになります。
\(y=\sinθ\),\(y=\cosθ\)のグラフの形の曲線を正弦曲線とよびます。
②グラフの対称性
\(y=f(x)\)について
\(f(-x)=-f(x)\) が成り立つとき、\(f(x)\)は奇関数
\(f(-x)=f(x)\) が成り立つとき、\(f(x)\)は偶関数
といいます。
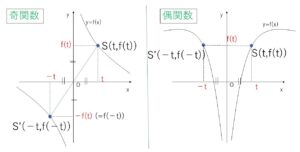
奇関数は\(S(t,f(t))\)に対して、\(S'(-t,f(-t))\)を考えると、
\(S'(-t,f(-t))\)\(=(-t,-f(t))\) が成り立ち、\(S\)の\(x\)座標の符号を変えると\(y\)座標の符号も変わるので、原点対称のグラフとなります。
偶関数は\(S(t,f(t))\)に対して、\(S'(-t,f(-t))\)を考えると、
\(S'(-t,f(-t))\)\(=(-t,f(t))\) が成り立ち、\(S\)の\(x\)座標の符号を変えても\(y\)座標が変わらないことから、\(y\)軸対称のグラフとなります。
\(\sin(-θ)=-\sinθ\), \(\cos(-θ)=\cosθ\) より
\(y=\sinθ\) は奇関数(原点対称なグラフ)、
\(y=\cosθ\) は偶関数(\(y\)軸対称なグラフ) となります。
③周期性
\(f(x+p)=f(x)\) (\(p\)は\(0\)でない定数) がすべての実数\(x\)について成り立つとき、\(f(x)\)は\(p\)を周期とする周期関数といいます。
\(f(x+2p)=f((x+p)+p)=f(x+p)=f(x)\) より、\(2p\)も周期であり、同様に\(3p,4p,-p,-2p\)なども周期となり、周期は無数に存在することになります。
そこで通常、周期は正の最小値の値をとります。
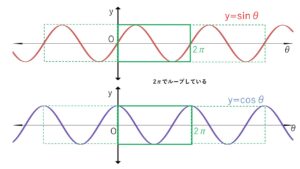
\(\sin(θ+2π)=\sinθ\), \(\cos(θ+2π)=\cosθ\) より
\(y=\sinθ\), \(y=\cosθ\) のどちらも周期が\(2π\) の周期関数となります。
続いて \(y=\tanθ\) についても同じように検討していきます。
①グラフの形状
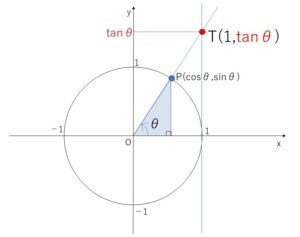
角\(θ\)の動径と単位円の交点を\(P\)とすると、\(tanθ\)は\(OP\)の傾きとなります。よって直線\(OP\)と\(x=1\)の交点を\(T\)とすると、\(T\)の\(y\)座標が\(\tanθ\)となり、これを利用すると\(\tanθ\)のグラフを描くことができます。
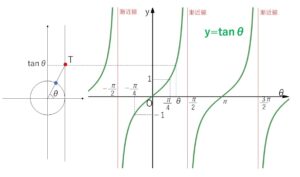
①\(θ\)が\(0→\displaystyle\frac{π}{2}\)のとき、傾き(\(\tanθ\))は\(0\)から上がり続け、\(\displaystyle\frac{π}{2}\)に近いと傾きは非常に大きな値となります。
\(θ=\displaystyle\frac{π}{2}\)では\(\tanθ\)は定義されず、
②\(θ\)が\(\displaystyle\frac{π}{2}→π→\displaystyle\frac{3}{2}π\)のとき、傾きは非常に小さい値(非常に急)→\(0\)→非常に大きい値 と変化します。
\(y=\tanθ\)の値域は、すべての実数値
そして \(y=\tanθ\) のグラフの形の曲線を正接曲線といいます。
また、\(θ=\displaystyle\frac{π}{2}\)付近での\(y=\tanθ\)のグラフは
\(\displaystyle\frac{π}{2}\)よりも小さい値から\(\displaystyle\frac{π}{2}\)に近づけると、グラフは直線 \(θ=\displaystyle\frac{π}{2}\) に限りなく近づき、
\(\displaystyle\frac{π}{2}\)よりも大きい値から\(\displaystyle\frac{π}{2}\)に近づけても、グラフは直線 \(θ=\displaystyle\frac{π}{2}\) に限りなく近づきます。
このように曲線が一定の直線に限りなく近づくとき、その直線を曲線の漸近線とよびます。
他にも、\(θ=-\displaystyle\frac{3π}{2},-\displaystyle\frac{π}{2},\displaystyle\frac{3π}{2},\displaystyle\frac{5π}{2}\)\(・・・\) なども漸近線であり、まとめると
\(θ=\displaystyle\frac{π}{2}+nπ\) (\(n\)は整数) が漸近線となります。
②グラフの対称性
\(\tan(-θ)=-\tanθ\) より
\(y=\tanθ\) は奇関数(グラフは原点対称)です。
③周期性
\(\tan(θ+π)=\tanθ\) より
周期が\(π\)の周期関数です。
・まとめ
・どちらも値域は \(-1≦y≦1\)
・どちらも周期が\(2π\)の周期関数
・\(y=\sinθ\)は奇関数(原点対称なグラフ) で、\(y=\cosθ\) は偶関数(\(y\)軸対称なグラフ)
・値域は実数全体
・周期が\(π\)の周期関数
・奇関数(原点対称なグラフ)
・\(θ=\displaystyle\frac{π}{2}+nπ\) (\(n\)は整数) を漸近線にもつ
今回例題はありません。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→三角関数のグラフ② back→三角関数の周期性と公式