引き続き三角方程式・不等式について見ていきます。
今回は\(θ\)の部分が \(kθ+α\) になっているケースです。
(例題)
\(0≦θ<2π\) のとき、次の方程式・不等式を解け。
(1)\(\sin2θ=\displaystyle\frac{\sqrt{3}}{2}\)
(2)\(\sqrt{2}\sin(θ+\displaystyle\frac{π}{3})=1\)
(3)\(2\cos(2θ+\displaystyle\frac{π}{4})≧\sqrt{3}\)
例えば(1)では、\(2θ=α\) とでもおけば、\(\sinα=\displaystyle\frac{\sqrt{3}}{2}\) となり簡単に解くことができます。
ただし、\(2θ(=α)\)の範囲に注意してください。\(0≦θ<2π\) なので、\(0≦2θ<4π\) で単位円2周分になります。(2)(3)も同様に範囲に注意です。
(解答)
慣れれば置き換えずにそのまま解いても構いません。
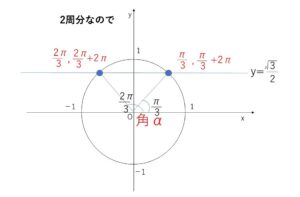
(1)\(2θ=α\) とおくと、、\(\sinα=\displaystyle\frac{\sqrt{3}}{2}\)・・・①
\(0≦θ<2π\) なので、\(0≦α(=2θ)<4π\)
よって①を満たす\(α\)は
\(α=\displaystyle\frac{π}{3},\displaystyle\frac{2}{3}π\), \(\displaystyle\frac{π}{3}+2π\), \(\displaystyle\frac{2}{3}π+2π\)
したがって
\(2θ=\displaystyle\frac{π}{3}\), \(\displaystyle\frac{2}{3}π\), \(\displaystyle\frac{7}{3}π\), \(\displaystyle\frac{8}{3}π\) より
\(θ=\displaystyle\frac{π}{6}\), \(\displaystyle\frac{π}{3}\), \(\displaystyle\frac{7}{6}π\), \(\displaystyle\frac{4}{3}π\)
(2)
\(\sqrt{2}\sin(θ+\displaystyle\frac{π}{3})=1\) より
\(\sin(θ+\displaystyle\frac{π}{3})=\displaystyle\frac{1}{\sqrt{2}}\)
\(θ+\displaystyle\frac{π}{3}=α\) とおくと
\(\sinα=\displaystyle\frac{1}{\sqrt{2}}\)・・・②
\(0≦θ<2π\) なので
\(\displaystyle\frac{π}{3}≦α<\displaystyle\frac{7π}{3}\)・・・③
よって単純に、\(α=\displaystyle\frac{π}{4}\)を解にしてはいけません。この解は範囲に入っていないからです。
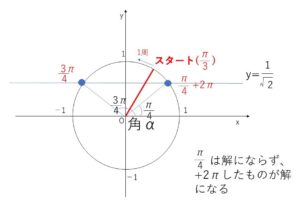
③の範囲で②を満たす\(α\)は、
\(α=\)\(\displaystyle\frac{3}{4}π,\displaystyle\frac{9}{4}π\)
よって
\(θ+\displaystyle\frac{π}{3}=\)\(\displaystyle\frac{3}{4}π,\displaystyle\frac{9}{4}π\) だから
\(θ=\displaystyle\frac{5}{12}π,\displaystyle\frac{23}{12}π\)
(3)
\(2\cos(2θ+\displaystyle\frac{π}{4})≧\sqrt{3}\) より
\(\cos(2θ+\displaystyle\frac{π}{4})≧\displaystyle\frac{\sqrt{3}}{2}\)
\(2θ+\displaystyle\frac{π}{4}=α\) とおくと
\(\cosα≧\displaystyle\frac{\sqrt{3}}{2}\)・・・④
\(0≦θ<2π\) より \(0≦2θ<4π\) だから
\(\displaystyle\frac{π}{4}≦2θ+\displaystyle\frac{π}{4}<\displaystyle\frac{17π}{4}\)
よって
\(\displaystyle\frac{π}{4}≦α<\displaystyle\frac{17π}{4}\)・・・⑤
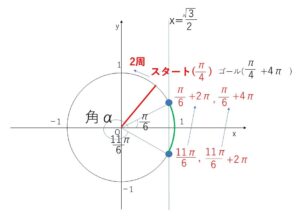
⑤の範囲で④を満たす\(α\)の範囲は
\(\displaystyle\frac{11}{6}π≦α≦\displaystyle\frac{13}{6}π\), \(\displaystyle\frac{23}{6}π≦α≦\displaystyle\frac{25}{6}π\)
よって
\(\displaystyle\frac{11}{6}π≦2θ+\displaystyle\frac{π}{4}≦\displaystyle\frac{13}{6}π\), \(\displaystyle\frac{23}{6}π≦2θ+\displaystyle\frac{π}{4}≦\displaystyle\frac{25}{6}π\)
\(\displaystyle\frac{19}{12}π≦2θ≦\displaystyle\frac{23}{12}π\), \(\displaystyle\frac{43}{12}π≦2θ≦\displaystyle\frac{47}{12}π\)
したがって
\(\displaystyle\frac{19}{24}π≦θ≦\displaystyle\frac{23}{24}π\), \(\displaystyle\frac{43}{24}π≦θ≦\displaystyle\frac{47}{24}π\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとございました。
next→三角方程式・不等式③ back→三角方程式・不等式①