三角関数の加法定理について見ていきます。
・加法定理
角の和や差の三角関数について、次の加法定理が成り立ちます。
\(\sin(α+β)\)\(=\sinα\cosβ\)\(+\cosα\sinβ\)
\(\sin(α-β)\)\(=\sinα\cosβ\)\(-\cosα\sinβ\)
[2]余弦
\(\cos(α\)\(+\)\(β)\)\(=\cosα\cosβ\)\(-\)\(\sinα\sinβ\)
\(\cos(α\)\(-\)\(β)\)\(=\cosα\cosβ\)\(+\)\(\sinα\sinβ\)・・・(※)
[3]正接
\(\tan(α+β)\)\(=\)\(\displaystyle\frac{\tanα+\tanβ}{1\color{blue}{-}\tanα\tanβ}\)
\(\tan(α-β)\)\(=\)\(\displaystyle\frac{\tanα-\tanβ}{1\color{blue}{+}\tanα\tanβ}\)
(証明)
「\(\cos(α-β)\)・・・(※) を示す→残りの\(\sin,\cos\)を示す→\(\tan\)を示す」
となります。
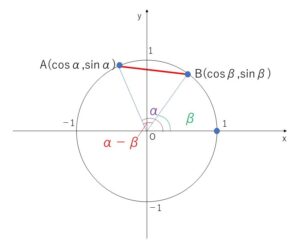
図のように単位円上に\(A(\cosα,\sinα)\)\(B(\cosβ,\sinβ)\) をとる。
2点 \(A,B\)間の距離の2乗は
\(AB^2\)\(=(\cosα-\cosβ)^2\)\(+(\sinα-\sinβ)^2\)・・・①
次に2点\(A,B\)を\(B\)が\(B'(1,0)\)にくるように原点まわりに\(-β\)回転させる。
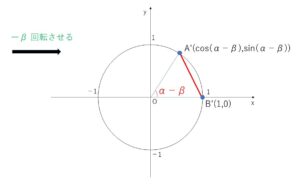
\(A\)の移動後の点\(A’\)の座標は\((\cos(α-β),\sin(α-β))\)
\(A,B\)は同じだけ移動するので、移動後の\(A’B’\)と移動前の\(AB\)の距離は同じである。
2点 \(A’,B’\)間の距離の2乗は
\(A’B’^2\)\(=\{(\cos(α-β)-1\}^2\)\(+\sin^2(α-β)\)・・・②
①②と\(AB^2=A’B’^2\) より
\((\cosα-\cosβ)^2\)\(+(\sinα-\sinβ)^2\)\(=\{(\cos(α-β)-1\}^2\)\(+\sin^2(α-β)\)
(左辺)
\(=\cos^2α-2\cosα\cosβ+\cos^2β\)\(+\sin^2α\)\(-2\sinα\sinβ\)\(+\sin^2β\)
\(=(\cos^2α+\sin^2α)\)\(+(\cos^2β+\sin^2β)\)\(-2\cosα\cosβ\)\(-2\sinα\sinβ\)
\(=2\)\(-2\cosα\cosβ\)\(-2\sinα\sinβ\)
(右辺)
\(=\cos^2(α-β)-2\cos(α-β)\)\(+1\)\(+\sin^2(α-β)\)
\(=\cos^2(α-β)+\sin^2(α-β)\)\(+1\)\(-2\cos(α-β)\)
\(=2-2\cos(α-β)\)
したがって
\(2\)\(-2\cosα\cosβ\)\(-2\sinα\sinβ\)\(=2-2\cos(α-β)\)
整理して
\(\cos(α-β)\)\(=\cosα\cosβ\)\(+\sinα\sinβ\)・・・(※)
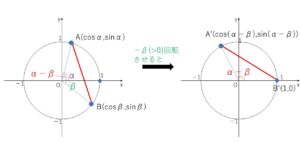
次に(※)において \(β→-β\) と置き換えると
\(\cos\{α-(-β)\}\)\(=\cosα\cos(-β)\)\(+\sinα\sin(-β)\)
\(\cos(-β)=\cosβ\), \(\sin(-β)=-\sinβ\) だから
\(\cos(α+β)\)\(=\cosα\cosβ\)\(-\sinα\sinβ\)
\(\cos\)の証明ができているので、\(\sin\)を\(\cos\)に変換する公式
\(\sinθ=\cos(\displaystyle\frac{π}{2}-θ)\) を利用します。
続いて
\(\sin(α+β)\)
\(=\cos\{\displaystyle\frac{π}{2}-(α+β)\}\)
\(=\cos\{(\displaystyle\frac{π}{2}-α)-β\}\)
(※)より
\(=\cos(\displaystyle\frac{π}{2}-α)\cosβ\)\(+\sin(\displaystyle\frac{π}{2}-α)\sinβ\)
\(=\sinα\cosβ\)\(+\cosα\sinβ\)
よって
\(\sin(α+β)\)\(=\sinα\cosβ\)\(+\cosα\sinβ\)・・・(X)
さらに(X)で \(β→-β\) と置き換えて
\(\sin(α-β)\)\(=\sinα\cos(-β)\)\(+\cosα\sin(-β)\)
ゆえに
\(\sin(α-β)\)\(=\sinα\cosβ\)\(-\cosα\sinβ\)
今までに示した\(\sin,\cos\)の加法定理を利用します。
最後に
\(\tan(α+β)\)
\(=\displaystyle\frac{\sin(α+β)}{\cos(α+β)}\)
\(=\displaystyle\frac{\sinα\cosβ+\cosα\sinβ}{\cosα\cosβ-\sinα\sinβ}\)
(分母分子を\(\cosα\cosβ\)で割ると)
\(=\displaystyle\frac{\displaystyle\frac{\sinα}{\cosα}+\displaystyle\frac{\sinβ}{\cosβ}}{1-\displaystyle\frac{\sinα\cdot\sinβ}{\cosα\cdot\cosβ}}\)
\(=\displaystyle\frac{\tanα+\tanβ}{1-\tanα\tanβ}\)
よって
\(\tan(α+β)\)\(=\displaystyle\frac{\tanα+\tanβ}{1-\tanα\tanβ}\)・・・(Y)
(Y)で\(β→-β\) と置き換えると
\(\tan(α-β)\)\(=\displaystyle\frac{\tanα+\tan(-β)}{1-\tanα\tan(-β)}\)
\(\tan(-β)=-\tanβ\) だから
\(\tan(α-β)\)\(=\displaystyle\frac{\tanα-\tanβ}{1+\tanα\tanβ}\)
しかし過去にこの加法定理の証明が入試で出題されたことがあるのでやはり使う公式の証明はできるようにしておくべきでしょう。
加法定理を利用する簡単な例題をやってみます。
(例題)次の値を求めよ。
(1)\(\sin\displaystyle\frac{π}{12}\) (2)\(\cos\displaystyle\frac{5}{12}π\) (3)\(\tan\displaystyle\frac{7}{12}π\)
(解答)
(1)
知っている角の値を使って加法定理により求めます。\(\displaystyle\frac{π}{4}\),\(\displaystyle\frac{π}{6}\) の差をとって
\(\displaystyle\frac{π}{12}=\displaystyle\frac{π}{4}-\displaystyle\frac{π}{6}\) (\(15°=45°-30°\)) を利用します。
\(\sin\displaystyle\frac{π}{12}\)
\(=\sin(\displaystyle\frac{π}{4}-\displaystyle\frac{π}{6})\)
\(=\sin\displaystyle\frac{π}{4}\cos\displaystyle\frac{π}{6}\)\(-\cos\displaystyle\frac{π}{4}\sin\displaystyle\frac{π}{6}\)
\(=\displaystyle\frac{1}{\sqrt{2}}・\displaystyle\frac{\sqrt{3}}{2}\)\(-\displaystyle\frac{1}{\sqrt{2}}・\displaystyle\frac{1}{2}\)
\(=\)\(\displaystyle\frac{\sqrt{6}-\sqrt{2}}{2}\)
(2)
\(\cos\displaystyle\frac{5}{12}π\)\(=\sin(\displaystyle\frac{π}{2}-\displaystyle\frac{5}{12}π)\)\(=\sin\displaystyle\frac{π}{12}\) なので(1)と同じ値になりますが、せっかくなので加法定理で求めてみます。
\(\cos\displaystyle\frac{5}{12}π\)
\(=\cos(\displaystyle\frac{π}{4}+\displaystyle\frac{π}{6})\)
\(=\cos\displaystyle\frac{π}{4}\cos\displaystyle\frac{π}{6}\)\(-\sin\displaystyle\frac{π}{4}\sin\displaystyle\frac{π}{6}\)
\(=\displaystyle\frac{1}{\sqrt{2}}\)\(・\displaystyle\frac{\sqrt{3}}{2}\)\(-\displaystyle\frac{1}{\sqrt{2}}・\displaystyle\frac{1}{2}\)
\(=\)\(\displaystyle\frac{\sqrt{6}-\sqrt{2}}{2}\)
(3)
\(\tan\displaystyle\frac{7}{12}π\)
\(=\tan(\displaystyle\frac{π}{4}+\displaystyle\frac{π}{3})\)
\(=\displaystyle\frac{\tan\displaystyle\frac{π}{4}+\tan\displaystyle\frac{π}{3}}{1-\tan\displaystyle\frac{π}{4}\tan\displaystyle\frac{π}{3}}\)
\(=\displaystyle\frac{1+\sqrt{3}}{1-1\cdot\sqrt{3}}\)
\(=\displaystyle\frac{(1+\sqrt{3})(1+\sqrt{3})}{(1-\sqrt{3})(1+\sqrt{3})}\)
\(=\displaystyle\frac{(1+\sqrt{3})^2}{-2}\)
\(=\)\(-2-\sqrt{3}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→加法定理② back→三角方程式・不等式③