三角関数の合成

\(a\sinθ+b\cosθ\) の形の式を、\(r\sin(θ+α)\) の形に変形する方法について見ていきます。

・三角関数の合成
加法定理を利用して、
\(a\sinθ+b\cosθ\)\(=r\sin(θ+α)\) の形に変形することを考えると、

\(r\sin(θ+α)\)
\(=r\sinθ\cosα+r\cosθ\sinα\)
\(=\)\(r\cosα\)\(\sinθ\)\(+r\sinα\)\(\cosθ\)
\(=\)\(a\)\(\sinθ\)\(+b\)\(\cosθ\)

だから、
\(r\cosα=a\),　\(r\sinα=b\)　・・・①

よって、\(r\)と\(α\)についての関係式は、
①より両辺の2乗の和をとって
\(r^2\cos^2α+r^2\sin^2α\)\(=a^2+b^2\)
\(∴\)　\(r=\sqrt{a^2+b^2}\)

また、①より
\(\cosα=\displaystyle\frac{a}{r}\)
\(\sinα=\displaystyle\frac{b}{r}\) 　なので

\(\cosα=\displaystyle\frac{a}{\sqrt{a^2+b^2}}\)
\(\sinα=\displaystyle\frac{b}{\sqrt{a^2+b^2}}\)

そして以上のことを図で視覚的に表すと次のようになります。

・三角関数の合成
\(a\sinθ+b\cosθ\)\(=\sqrt{a^2+b^2}\sin(θ+α)\)
ただし
\(\cosα=\displaystyle\frac{a}{\sqrt{a^2+b^2}}\)
\(\sinα=\displaystyle\frac{b}{\sqrt{a^2+b^2}}\)

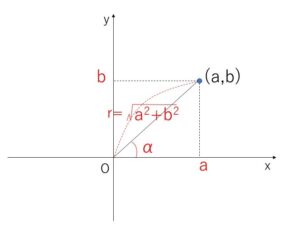
実際に合成する際には、この図を描いて\(r\)や\(α\)を決定していくことになります。

同様に、\(a\sinθ+b\cosθ\)を \(r\cos(θ-β)\) の形に変形することもできますが、これは例題で扱っていきます。(\(-β\) なっているのは、\(\cos(θ+β)\)のほうだと、加法定理の2項目に－がついているのでそれを避けているのですが、\(+β\)ではダメというわけではないです)

それと三角関数の合成のポイントを少しだけ。

(例題1)次の式を \(r\sin(kθ+α°)\) の形にせよ。
(1)\(2\sqrt{3}\sin2θ-2\cos2θ\)
(2)\(\sin(θ+30°)+\cos(θ-60°)\)

(解答)
(1)
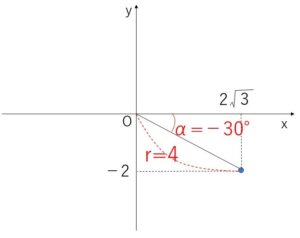
\(r=\sqrt{(2\sqrt{3})^2+(-2)^2}\)\(=4\)
また
\(\cosα=\displaystyle\frac{2\sqrt{3}}{4}\)\(=\displaystyle\frac{\sqrt{3}}{2}\)
\(\sinα=\displaystyle\frac{-2}{4}\)\(=-\displaystyle\frac{1}{2}\)
より、\(α=-30°\)

したがって
\(2\sqrt{3}\sin2θ-2\cos2θ\)
\(=4\sin(2θ-30°)\)

(2)
(角が違うのでまず加法定理により統一します)

\(\sin(θ+30°)+\cos(θ-60°)\)
\(=\sinθ\displaystyle\cdot\frac{\sqrt{3}}{2}+\cosθ\cdot\displaystyle\frac{1}{2}\)\(+\cosθ\cdot\displaystyle\frac{1}{2}+\sinθ\cdot\displaystyle\frac{\sqrt{3}}{2}\)
\(=\sqrt{3}\sinθ+\cosθ\)

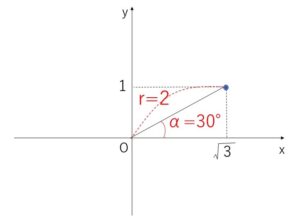
\(r=\sqrt{(\sqrt{3})^2+1}\)\(=2\)

\(\cosα=\displaystyle\frac{\sqrt{3}}{2}\)
\(\sinα=\displaystyle\frac{1}{2}\) より
\(α=30°\)

よって
(与式)
\(=2\sin(θ+30°)\)

(例題2)
\(\sqrt{2}\cosθ-\sqrt{6}\sinθ\)\(=r\cos(θ+α°)\)　となる \(r,\)\(α\)を求めよ。
(ただし\(r>0\),　\(0°≦α°<360°\))

(解答1)
\(r\cos(θ+α)\)
\(=r\cosθ\cosα-r\sinθ\sinα\)
\(=r\cosα\cosθ-r\sinα\sinθ\)
\(=\sqrt{2}\cosθ-\sqrt{6}\sinθ\)

3,4行目を比較して
\(r\cosα=\sqrt{2}\),　\(r\sinα=\sqrt{6}\)・・・①

①の両辺を2乗して和をとると
\(r^2=2+6=8\)
\(r=2\sqrt{2}\)

また①より
\(\cosα=\displaystyle\frac{1}{2}\),　\(\sinα=\displaystyle\frac{\sqrt{3}}{2}\) より
\(α=60°\)

(\(\sqrt{2}\cosθ-\sqrt{6}\sinθ\)\(=2\sqrt{2}\cos(θ+60°)\) となる)

(解答2)
\(\sin\)へと合成すると(詳細は略)

\(\sqrt{2}\cosθ-\sqrt{6}\sinθ\)
\(=-\sqrt{6}\sinθ+\sqrt{2}\cosθ\)
\(=2\sqrt{2}\sin(θ+150°)\)

ここで \(\sin(x+90°)\)\(=\cos x\) より
\(\sin(θ+150°)\)
\(=\sin(θ+60°+90°)\)
\(=\cos(θ+60°)\)

したがって
\(\sqrt{2}\cosθ-\sqrt{6}\sinθ\)
\(=2\sqrt{2}\cos(θ+60°)\)

\(r=2\sqrt{2}\),　\(α=60°\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角方程式・不等式(合成)　back→積和・和積の公式の利用②