三角方程式の解の個数を分類する問題について見ていきます。
三角関数\(\sinθ\)または\(\cosθ\)を\(t\)と文字でおいたときに、\(t\)1つに対応する\(θ\)の個数に注意することがポイントです。
(例題)
\(a\)を定数とする。\(θ\)に関する方程式
\(\cos^2θ-\sinθ+a+1=0\)
について次の問に答えよ。ただし \(0≦θ<2π\) とする。
(1)この方程式が解をもつための\(a\)の条件を求めよ。
(2)この方程式の解の個数を\(a\)の値の範囲によって調べよ。
(解答)
(1)
\(\cos^2θ-\sinθ+a+1=0\) より
\(1-\sin^2θ-\sinθ+a+1=0\)
\(\sinθ=t\) とおいて整理すると
\(t^2+t-a-2=0\)・・・① (\(-1≦t≦1\))
\(t^2+t-2=a\)
と変形すると、左辺の関数を座標平面に固定することができるので、あとは
\(y=t^2+t-2\) と \(y=a=(定数)\) が共有点をもつ条件を考えます。\(y=a\)は\(x\)軸に平行な直線(横にまっすぐな直線)なので、\(a\)が変化してもただ上下するだけです。
\(t^2+t-2=a\) より
\(y=t^2+t-2\) (\(-1≦t≦1\))
\(y=a\)
が共有点をもつ \(a\)の範囲を考えればよい。
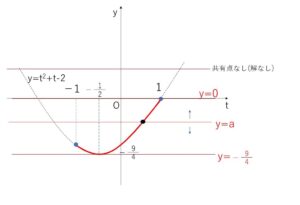
\(y=t^2+t-2\)
\(=(t+\displaystyle\frac{1}{2})^2-\displaystyle\frac{9}{4}\)
だから図より、
\(-\displaystyle\frac{9}{4}≦a≦0\)
(2)
ここで注意することは、もともとは\(θ\)の方程式で置き換えにより\(t\)の方程式にしているので、単純に(共有点の数)=(解\(θ\)の個数) とはならないことです。
例えば、\(a=-\displaystyle\frac{5}{4}\) のとき、\(t\)としての解は(共有点の\(t\)座標は)、\(t=\displaystyle\frac{1}{2}\) ですが、それに対応する\(θ\)を求めると、\(t=\sinθ=\displaystyle\frac{1}{2}\) の解は、\(θ=\displaystyle\frac{π}{6},\displaystyle\frac{5π}{6}\)の2つになるので、共有点1つに対して2個の解\(θ\)が存在することになります。
一方、\(a=0\) のときは \(t=1\) が\(t\)としての解で、それに対応する\(θ\)は、 \(t=\sinθ=1\) より \(θ=\displaystyle\frac{π}{2}\) の1つだけで、共有点1つに対して1個の解\(θ\)が存在することになります。
1次式の三角方程式を解くときを思い出すと、\(θ\)が1周分なら
\(t=\sinθ=±1\) のときだけ、対応する\(θ\)が1つになり、他は対応する\(θ\)が2つになるので、
\(t=±1\)のときだけ共有点の数がそのまま解\(θ\)の個数で、それ以外は 共有点の数の2倍が解\(θ\)の個数となります。
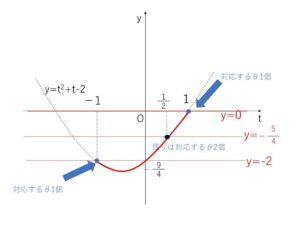
グラフより
(i)\(a=0\) のとき 共有点1個 \(t\)座標は \(t=1\)
(ii)\(-2<a<0\) のとき 共有点1個 \(t\)座標は \(t≠±1\)
(iii)\(a=-2\) のとき 共有点2個
2共有点のうち 1つの\(t\)座標は\(t=-1\) もう一方は \(t≠1\)
(iv)\(-\displaystyle\frac{9}{4}<a<-2\) のとき 共有点2個
2個とも\(t\)座標は \(t≠±1\)
(v)\(a=-\displaystyle\frac{9}{4}\) のとき 共有点1個
\(t\)座標は \(t≠±1\)
\(t=\sinθ=±1\) が共有点の\(t\)座標のとき、\(t\)1つに対して\(θ\)1つ
それ以外は \(t\)1つに対して\(θ\)2つが対応することに注意すると
\(a>0\), \(a<-\displaystyle\frac{9}{4}\) 0個
\(a=0\) 1個
\(-2<a<0\) 2個
\(a=-2\) 3個
\(-\displaystyle\frac{9}{4}<a<-2\) 4個
\(a=-\displaystyle\frac{9}{4}\) 2個
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角関数の図形への応用 back→円の媒介変数表示