正四面体の切り口の面積

→高校数学TOP

正四面体を平面で切ったときの切り口の面積を求めます。

(問題)
1辺の長さが\(1\)の正四面体\(OABC\)がある。辺\(OA\)の中点を\(L\)、辺\(OB\)を\(2:1\)の比に内分する点を\(M\)、辺\(OC\)を\(1:2\)の比に内分する点を\(N\)とする。\(△LNM\)の面積を求めよ。

(解答)

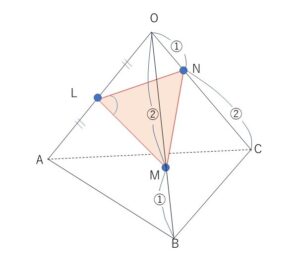
\(△OLM\)に余弦定理を用いると
\(LM^2=(\displaystyle\frac{1}{2})^2+(\displaystyle\frac{2}{3})^2-2・\displaystyle\frac{1}{2}・\displaystyle\frac{2}{3}・\cos60°\)
よって　\(LM^2=\displaystyle\frac{13}{36}\)

\(△OMN\)に余弦定理を用いると
\(MN^2=(\displaystyle\frac{2}{3})^2+(\displaystyle\frac{1}{3})^2-2・\displaystyle\frac{2}{3}・\displaystyle\frac{1}{3}・\cos60°\)
よって　\(MN^2=\displaystyle\frac{3}{9}\)

\(△ONL\)に余弦定理を用いると
\(NL^2=(\displaystyle\frac{1}{3})^2+(\displaystyle\frac{1}{2})^2-2・\displaystyle\frac{1}{3}・\displaystyle\frac{1}{2}・\cos60°\)
よって　\(NL^2=\displaystyle\frac{7}{36}\)

ゆえに、\(LM=\displaystyle\frac{\sqrt{13}}{6},MN=\displaystyle\frac{\sqrt{3}}{3},NL=\displaystyle\frac{\sqrt{7}}{6}\)

また、\(△LMN\)において余弦定理より
\(\cos\angle MLN=\displaystyle\frac{\displaystyle\frac{13}{36}+\displaystyle\frac{7}{36}-\displaystyle\frac{3}{9}}{2・\displaystyle\frac{\sqrt{13}}{6}・\displaystyle\frac{\sqrt{7}}{6}}\)\(=\displaystyle\frac{4}{\sqrt{91}}\)

\(0°<\angle MLN<180°\) より
\(\sin\angle MLN=\sqrt{1-(\displaystyle\frac{4}{\sqrt{91}})^2}\)\(=\displaystyle\frac{5\sqrt{3}}{\sqrt{91}}\)

したがって
\(△LMN=\displaystyle\frac{1}{2}・LM・LN・\sin\angle MLN\)
\(=\displaystyle\frac{1}{2}・\displaystyle\frac{\sqrt{13}}{6}・\displaystyle\frac{\sqrt{7}}{6}・\displaystyle\frac{5\sqrt{3}}{\sqrt{91}}\)
\(=\)\(\displaystyle\frac{5\sqrt{3}}{72}\)