今回から整式の除法、つまり割り算について学んでいきます。
・整式の除法
同じ1つの文字についての(例えば\(x\)など)、2つの整式\(A,B\)において、\(A\)を\(B\)で割ったときの商を\(Q\)、余りを\(R\)とすると、
\(A=BQ+R\) (\(R\)の次数\(<B\)の次数) (\(B≠0\))
が成り立ちます。
特に余りが\(0\)のとき、つまり\(R=0\)のときは「\(A\)は\(B\)で割り切れる」といいます。
整数の割り算 \(a=bq+r\) (\(0≦r<b\))と同様の考え方です。
ただし、余りについての定義が違うことに注意してください。
整式の場合は次数に着目していて、整数の場合は\(0\)以上で\(b\)より小さい数です。
ただし、余りについての定義が違うことに注意してください。
整式の場合は次数に着目していて、整数の場合は\(0\)以上で\(b\)より小さい数です。
実際に割り算をするときは、普通の数字と同様に筆算で計算します。
例題を見ていきましょう。
(例題1)
\((5x^2-3x^3+4)\)\(÷(3x^2+x-1)\) の商と余りを求めよ。
整式の割り算をするときは
①降べきの順に整理する
②欠けている次数の項は空白にしておく
③余りが割る数\(B\)よりも次数が低くなるまで計算する
に注意してください。
①について、\(5x^2-3x^3+4\)を\(-3x^3+5x^2+4\)と整理します。
②について、\(-3x^3+5x^2+4\)は次数1の項が無いので空白にしておきます。
(解答)
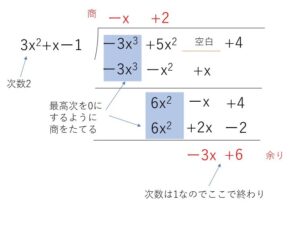
商 \(-x+2\) 余り \(-3x+6\)
(例題2)
\(4x^2+3xy+2y^2\)を\(x+2y\)で割って、商と余りを求めたい。
(1)\(x\)の整式とみて求めよ。
(2)\(y\)の整式とみて求めよ。
(1)(2),それぞれの文字について降べきの順に整理します。
(1)では\(y\)は定数扱い、(2)では\(x\)は定数扱いになります。
(1)では\(y\)は定数扱い、(2)では\(x\)は定数扱いになります。
(解答)
(1)
\(x\)について整理する。
\((4x^2+3yx+2y^2)\)\(÷(x+2y)\)を計算すればよい。
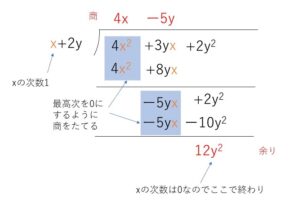
商 \(4x-5y\) 余り \(12y^2\)
(2)\(y\)について整理する。
\((2y^2+3xy+4x^2)\)\(÷(2y+x)\)を計算すればよい。
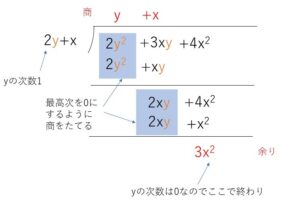
商 \(y+x\) 余り \(3x^2\)
このように変数が1つでないとき、余りが\(0\)でない場合は、着目する文字によって商も余りも異なることがあります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→A=BQ+R の利用