自然数\(n\)と互いに素である\(n\)以下の自然数の個数の数え上げの問題について考えていきます。
個数の数え上げなので、集合の要素の個数の知識も合わせて利用します。
(例題1)
\(n\)を自然数とする。\(m≦n\)で \(m\) と \(n\) が互いに素であるような自然数\(m\)の個数を\(f(n)\) とするとき、次の問いに答えよ。
(1)\(f(15)\) を求めよ。
(2)\(f(pq)\) を求めよ。ただし、\(p,q\)は異なる素数とする。
(3)\(f(p^k)\) を求めよ。ただし、\(p\)は素数、\(k\)は自然数とする。
(解答)
(1)
互いに素であるものの個数を直接数えるよりも、互いに素でないものの個数のほうが数えやすいことに着目します。\(15=3×5\) なので、\(3\)の約数をもつ数、つまり\(3\)の倍数の数はすぐにわかります。\(5\)の約数をもつものも同様です。 これら\(3,5\)の倍数が\(f(15)\)でないものなので、全体の数\(15\)(個)から除けば答えが出ます。ただし、\(3\)かつ\(5\)の倍数つまり\(15\)の倍数である\(15\)は重複して数えないように。
\(3,6,9,12,15,5,10\) の\(7\) 個
\(p,q\)は異なる素数であるから、\(pq\)と互いに素でない自然数は、\(p\)の倍数または\(q\)の倍数なので、\(pq\)以下の自然数で考えると
\(p,2p,3p,・・・,(q-1)p,qp\) →\(q\)(個)
\(q,2q,3q,・・・,(p-1)q,pq\) →\(p\)(個)
である。\(pq\) が重複して考えられていることに注意して
\(f(pq)=pq-(q+p-1)\)\(=pq-p-q+1\)
\(=\)\((p-1)(q-1)\)
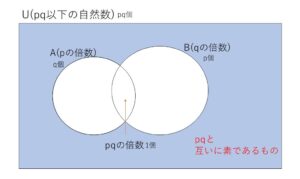
\(A\):\(p\)の倍数
\(B\):\(q\)の倍数
\(U\):\(pq\)以下の自然数
として、
全体\(U\)の個数\(n(U)\)から、\(p\)の倍数または\(q\)の倍数の個数\(n(A \cup B)\) を除くことを考えます。
\(n(A)=pq÷p=q\), \(n(B)=pq÷q=p\)
\(n(A \cap B)=pq÷pq=1\)
なので、
\(n(A \cup B)=n(A)+n(B)-n(A \cap B)=\)\(q+p-1\)
よって、
\(f(pq)=n(U)-n(A \cup B)\)\(=pq-(q+p-1)\)
\(=(p-1)(q-1)\)
\(p\)が素数なので、\(p^k\)以下の\(p\)の倍数を数えると
\(p^k÷p=p^{k-1}\) 個 ある。よって
以下発展的な内容です。
例題の\(f(n)\)はオイラー関数とよばれ、\(φ(n)\) で表されます。
しかし例題を解いたようにオイラー関数の知識がなくても問題は解けます。
ただ、オイラー関数の知識は、理解を深めるだけでなく、考え方もよい勉強になるので、余裕がある方は読んでみて下さい。
・オイラー関数
\(n\)を自然数とするとき、\(n\)以下の自然数で\(n\)と互いに素であるものの個数を\(φ(n)\)で表します。この\(φ(n)\)をオイラー関数とよびます。
①\(n\)が1つの素数のみの積で表される場合
\(p\)を素数、\(a\)を自然数とします。\(n\)が
\(n=p^a\)
で表されるとき、
\(n\)以下の\(p\)の倍数の個数は、\(p^a÷p=p^{a-1}\) (個)なので
\(φ(n)\)
\(=φ(p^a)\)
\(=p^a-p^{a-1}\) ←(例題(3)の答え)
\(=p^a(1-\displaystyle\frac{1}{p})\)
\(=n(1-\displaystyle\frac{1}{p})\)
②\(n\)が2つの素数の積で表される場合
\(p,q\)を素数、\(a,b\)を自然数とします。\(n\)が
\(n=p^aq^b\)
で表されるとき、
\(A\):\(p\)の倍数
\(B\):\(q\)の倍数
\(U\):\(p^aq^b\)以下の自然数
として、
全体\(U\)の個数\(n(U)\)から、\(p\)の倍数または\(q\)の倍数の個数\(n(A \cup B)\) を除くことを考えます。
\(n(A)=p^aq^b÷p=p^{a-1}q^b\)
\(n(B)=p^aq^b÷q=p^aq^{b-1}\)
\(n(A \cap B)=p^aq^b÷pq=p^{a-1}q^{b-1}\)
なので、
\(n(A \cup B)=n(A)+n(B)-n(A \cap B)\)\(=p^{a-1}q^b+p^aq^{b-1}-p^{a-1}q^{b-1}\)
よって、
\(φ(n)\)
\(=φ(p^aq^b)\)
\(=n(U)-n(A \cup B)\)
\(=p^aq^b-\)\((p^{a-1}q^b+p^aq^{b-1}-p^{a-1}q^{b-1})\)
\(=p^aq^b(1-\displaystyle\frac{1}{p}-\displaystyle\frac{1}{q}\)\(+\displaystyle\frac{1}{pq})\)
\(=p^aq^b(1-\displaystyle\frac{1}{p})(1-\displaystyle\frac{1}{q})\)・・・(1)
\(=n(1-\displaystyle\frac{1}{p})(1-\displaystyle\frac{1}{q})\)
また(1)から
(1)\(=p^a(1-\displaystyle\frac{1}{p})q^b(1-\displaystyle\frac{1}{q})\)
\(=φ(p^a)φ(q^b)\) (上記素数が1つの場合①より)
とも表されます。
\(φ(pq)=pq(1-\displaystyle\frac{1}{p})(1-\displaystyle\frac{1}{q})\)\(=(p-1)(q-1)\) です。
例題(1)は、\(a=b=1\), \(p=3\),\(q=5\) の場合です。(1)より
\(φ(15)=φ(3×5)\)\(=15(1-\displaystyle\frac{1}{3})(1-\displaystyle\frac{1}{5})=8\) です。
③\(n\)が3つの素数の積で表される場合
\(p,q,r\)を素数、\(a,b,c\)を自然数とします。\(n\)が
\(n=p^aq^br^c\)
で表されるとき、
\(A\):\(p\)の倍数
\(B\):\(q\)の倍数
\(C\):\(r\)の倍数
\(U\):\(p^aq^br^c\)以下の自然数
として、
全体\(U\)の個数\(n(U)\)から、\(p\)の倍数または\(q\)の倍数または\(r\)の倍数の個数\(n(A \cup B \cup C)\) を除くことを考えます。
\(n(B)=p^aq^br^c÷q\)\(=p^aq^{b-1}r^c\)
\(n(C)=p^aq^br^c÷r\)\(=p^aq^{b}r^{c-1}\)
\(n(A \cap B)=p^aq^br^c÷pq\)\(=p^{a-1}q^{b-1}r^c\)
\(n(B \cap C)=p^aq^br^c÷qr\)\(=p^{a}q^{b-1}r^{c-1}\)
\(n(C \cap A)=p^aq^br^c÷rp\)\(=p^{a-1}q^{b}r^{c-1}\)
\(n(A \cap B \cap C)=p^aq^br^c÷pqr\)\(=p^{a-1}q^{b-1}r^{c-1}\)
\(n(A \cup B \cup C)\)
\(=n(A)+n(B)+n(C)\)\(-n(A \cap B)-n(B \cap C)-n(C \cap A)\)\(+n(A \cap B \cap C)\)
\(=p^{a-1}q^br^c+p^aq^{b-1}r^c+p^aq^{b}r^{c-1}\)\(-p^{a-1}q^{b-1}r^c-p^{a}q^{b-1}r^{c-1}\)\(-p^{a-1}q^{b}r^{c-1}\)\(+p^{a-1}q^{b-1}r^{c-1}\)
\(=p^aq^br^c(\displaystyle\frac{1}{p}+\displaystyle\frac{1}{q}+\displaystyle\frac{1}{r}\)\(-\displaystyle\frac{1}{pq}-\displaystyle\frac{1}{qr}-\displaystyle\frac{1}{rp}\)\(+\displaystyle\frac{1}{pqr})\)
\(=φ(p^aq^br^c)\)
\(=n(U)-n(A \cup B \cup C)\)
\(=p^aq^br^c-p^aq^br^c(\displaystyle\frac{1}{p}+\displaystyle\frac{1}{q}+\displaystyle\frac{1}{r}\)\(-\displaystyle\frac{1}{pq}-\displaystyle\frac{1}{qr}-\displaystyle\frac{1}{rp}\)\(+\displaystyle\frac{1}{pqr})\)
\(=p^aq^br^c(1-\displaystyle\frac{1}{p}-\displaystyle\frac{1}{q}-\displaystyle\frac{1}{r}\)\(+\displaystyle\frac{1}{pq}+\displaystyle\frac{1}{qr}+\displaystyle\frac{1}{rp}\)\(-\displaystyle\frac{1}{pqr})\)
\(=p^aq^br^c\{(1-\displaystyle\frac{1}{q}\)\(-\displaystyle\frac{1}{r}+\displaystyle\frac{1}{qr})\)\(-\displaystyle\frac{1}{p}(1-\displaystyle\frac{1}{q}\)\(-\displaystyle\frac{1}{r}+\displaystyle\frac{1}{qr})\}\) (\(p\)について整理)
\(=p^aq^br^c\{(1-\displaystyle\frac{1}{q})(1-\displaystyle\frac{1}{r})\)\(-\displaystyle\frac{1}{p}(1-\displaystyle\frac{1}{q})(1-\displaystyle\frac{1}{r})\}\)
\(=p^aq^br^c(1-\displaystyle\frac{1}{p})(1-\displaystyle\frac{1}{q})(1-\displaystyle\frac{1}{r})\)・・・(2)
\(=n(1-\displaystyle\frac{1}{p})(1-\displaystyle\frac{1}{q})(1-\displaystyle\frac{1}{r})\)
また(2)より
(2)\(=p^a(1-\displaystyle\frac{1}{p})q^b(1-\displaystyle\frac{1}{q})r^c(1-\displaystyle\frac{1}{r})\)
\(=φ(p^a)φ(q^b)φ(r^c)\) (素数が1個の場合①より)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。