合同式の方程式の解き方について見ていきます。
(例題)
次の方程式を満たす\(x\)を、それぞれの法\(p\)において、
\(x≡a\) (\(\mathrm{mod}\) \(p\))
の形で表せ。ただし\(a\)は、\(0≦a<p\) を満たす整数とする。
(1)\(x+3≡7\) (\(\mathrm{mod}\) \(9\))
(2)\(2x≡3\) (\(\mathrm{mod}\) \(5\))
(3)\(8x≡2\) (\(\mathrm{mod}\) \(10\))
(解答)
(1)
合同式の両辺に、余りが同じ数になる数を、足す・引く・掛ける ことができます。もちろん数そのものが同じでもよいので、両辺\(3\)を引いてみます。
以下、(\(\mathrm{mod}\) \(9\)) とする。
\(x+3-3≡7-3\)
\(x≡7-3\) (←等式と同じように移項ができることになる)
\(x≡4\) (\(\mathrm{mod}\) \(9\))
\(x+3-3≡7-3\)
\(x≡7-3\) (←等式と同じように移項ができることになる)
\(x≡4\) (\(\mathrm{mod}\) \(9\))
(2)
(解答①)左辺を変形して \(x≡\)の形にする方法
(解答①)左辺を変形して \(x≡\)の形にする方法
(\(\mathrm{mod}\) \(5\)) では、\(5\)の倍数は\(0\)なので、\(2x≡3\)の両辺を何倍(整数倍)かして、\(5\)の倍数を足し引きすることで、うまく\(x≡\)の形にもっていきます。\(2x×3=6x\) で\(6x-5x=x\)なので、\(3\)倍して\(5x\)を引けばよいことになります。
以下(\(\mathrm{mod}\) \(5\))とする。
両辺を\(3\)倍すると
\(6x≡9≡4\)
\(6x-5x≡4\)
よって \(x≡4\) (\(\mathrm{mod}\) \(5\))
両辺を\(3\)倍すると
\(6x≡9≡4\)
\(6x-5x≡4\)
よって \(x≡4\) (\(\mathrm{mod}\) \(5\))
(解答②)表を使う方法
具体的に\(x≡0,1,2,3,4\) (\(\mathrm{mod}\) \(5\)) のときの\(2x\)を計算して表でまとめてみます。
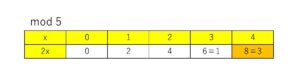
表より、\(2x≡3\) (\(\mathrm{mod}\) \(5\)) となるのは
\(x≡4\) (\(\mathrm{mod}\) \(5\))
\(x≡4\) (\(\mathrm{mod}\) \(5\))
(解答③)両辺を同じ数で割る方法(ただし法\(p\)と互いに素である数で割る)
法\(p\)と互いに素である数では割り算ができることを利用します。
→(3-1)合同式の性質 の除法参照。
→(3-1)合同式の性質 の除法参照。
以下(\(\mathrm{mod}\) \(5\))とする。
\(3≡8\) なので
\(2x≡8\) (\(\mathrm{mod}\) \(5\))
\(2x≡8\) (\(\mathrm{mod}\) \(5\))
\(2\)と\(5\)は互いに素であるので、両辺\(2\)で割って
\(x≡4\) (\(\mathrm{mod}\) \(5\))
\(x≡4\) (\(\mathrm{mod}\) \(5\))
(3)
(2)の解答①と同じ方法は使えません。
\(8\)を整数倍した数から、\(10\)の整数倍の数を足しひきして、\(1\)にできるかどうか考えるとすると、それは\(8k-10l=1\) を満たす整数\(k,l\)を見つけること同じで、この等式の左辺は偶数、右辺は奇数なので、 \(k,l\)は存在しないことになります。\(x\)の係数と法\(p\)が互いに素でない場合だとこうなります。
\(8\)を整数倍した数から、\(10\)の整数倍の数を足しひきして、\(1\)にできるかどうか考えるとすると、それは\(8k-10l=1\) を満たす整数\(k,l\)を見つけること同じで、この等式の左辺は偶数、右辺は奇数なので、 \(k,l\)は存在しないことになります。\(x\)の係数と法\(p\)が互いに素でない場合だとこうなります。
(解答①)表を使う方法
先ほどと同じで表を使う方法で解くことができます。

表より、\(8x≡2\) (\(\mathrm{mod}\) \(10\)) となるのは
\(x≡4,9\) (\(\mathrm{mod}\) \(10\))
\(x≡4,9\) (\(\mathrm{mod}\) \(10\))
(解答②)両辺を同じ数で割る方法(法\(p\)と互いに素でない数で割る方法)
\(2\)と法\(10\)は互いに素でないので単純に両辺\(2\)で割ることができませんが、\(8x≡2\) を見ると、等式と同じように\(2\)で割りたくなる人が多いと思うので、この解法も紹介します。結論から先に言うと、両辺\(2\)で割ると同時に、法\(10\)も\(2\)で割ればよいです。理由は後で説明します。
\(8x≡2\) (\(\mathrm{mod}\) \(10\)) より
\(4x≡1\) (\(\mathrm{mod}\) \(5\))
\(4x≡1\) (\(\mathrm{mod}\) \(5\))
両辺\(4\)倍して
\(16x≡4\) (\(\mathrm{mod}\) \(5\))
\(16x≡4\) (\(\mathrm{mod}\) \(5\))
\(16x-15x≡4\) (\(\mathrm{mod}\) \(5\))
よって\(x≡4\) (\(\mathrm{mod}\) \(5\))
あとは(\(\mathrm{mod}\) \(10\))に戻せばよいです。具体的に数字を考えてみます。
\(x≡4\) (\(\mathrm{mod}\) \(5\))のとき
\(x=4,9,4+10(=14)\)\(,9+10(=19)\)\(,4+20(=24),・・・\)\(4+10k,9+10k\)
だから
\(x≡4,9\) (\(\mathrm{mod}\) \(10\))
\(x≡4,9\) (\(\mathrm{mod}\) \(10\))
(参考)合同式の除法(互いに素でない数で割る場合)
\(ac≡bc\) (\(\mathrm{mod}\) \(p’c\))
\(\leftrightarrow\)
\(a≡b\) (\(\mathrm{mod}\) \(p’\))
\(\leftrightarrow\)
\(a≡b\) (\(\mathrm{mod}\) \(p’\))
(証明)
\(ac≡bc\) (\(\mathrm{mod}\) \(p’c\)) より
\(ac-bc=p’ck\) (\(k\)は整数) と表せる。
\(c(a-b)=p’ck\) だから
\(a-b=p’k\)
よって
\(a≡b\) (\(\mathrm{mod}\) \(p’\))
\(ac≡bc\) (\(\mathrm{mod}\) \(p’c\)) より
\(ac-bc=p’ck\) (\(k\)は整数) と表せる。
\(c(a-b)=p’ck\) だから
\(a-b=p’k\)
よって
\(a≡b\) (\(\mathrm{mod}\) \(p’\))
また逆にたどれば、
\(a≡b\) (\(\mathrm{mod}\) \(p’\)) \(\rightarrow\) \(ac≡bc\) (\(\mathrm{mod}\) \(p’c\))
が成り立つことも分かる。
\(a≡b\) (\(\mathrm{mod}\) \(p’\)) \(\rightarrow\) \(ac≡bc\) (\(\mathrm{mod}\) \(p’c\))
が成り立つことも分かる。
両辺と法の公約数\(c\)で両辺を割るときは、法も同時に割ればよいです。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。