ある自然数\(a,b\)の最大公約数を求めるときに、\(a,b\)自体の数が大きかったり、約数が見つかりにくい場合があります。そのときに有効なのがユークリッドの互除法です。
・ユークリッドの互除法に関する定理
2つの自然数\(a,b\)について、\(a\)を\(b\)で割ったときの商を\(q\)、余りを\(r\)とすると
\(a,b\)の最大公約数は、\(b,r\)の最大公約数と等しい。
\(a,b\)の最大公約数は、\(b,r\)の最大公約数と等しい。
(証明)
\(a=bq+r\)・・・① とする。
①より \(r=a-bq\)・・・②
\(a=bq+r\)・・・① とする。
①より \(r=a-bq\)・・・②
\(a,b\)の最大公約数を\(g\)、\(b,r\)の最大公約数を\(g’\)とする。
\(a=gm\), \(b=gn\) (\(m,n\)は互いに素である自然数) と表せるので②より
\(r=gm-gnq=g(m-nq)\)
よって\(g\)は\(r\)の約数なので、\(g\)は\(b,r\)の公約数である。
\(b,r\)の最大公約数が\(g’\)なので、\(g≦g’\)・・・③
\(r=gm-gnq=g(m-nq)\)
よって\(g\)は\(r\)の約数なので、\(g\)は\(b,r\)の公約数である。
\(b,r\)の最大公約数が\(g’\)なので、\(g≦g’\)・・・③
また、\(b,r\)の最大公約数は\(g’\)だから
\(b=g’k\), \(r=g’l\) (\(k,l\)は互いに素である自然数)と表せるので①より
\(a=g’kq+g’l=g'(kq+l)\)
\(b=g’k\), \(r=g’l\) (\(k,l\)は互いに素である自然数)と表せるので①より
\(a=g’kq+g’l=g'(kq+l)\)
よって\(g’\)は\(a\)の約数なので、\(g’\)は\(a,b\)の公約数である。
\(a,b\)の最大公約数が\(g\)なので、\(g’≦g\)・・・④
③④より、\(g=g’\)
つまり\(a,b\)の最大公約数は、\(b,r\)の最大公約数と等しい。
つまり\(a,b\)の最大公約数は、\(b,r\)の最大公約数と等しい。
なお、\(0≦r<b\) という条件は使っていないので、①の形になれば、この定理は成り立ちます。
・ユークリッドの互除法
上記定理を繰り返し使うことで、2数の最大公約数を求めることができます。
上記定理を繰り返し使うことで、2数の最大公約数を求めることができます。
\(a,b\)の最大公約数を求める方法 (\(a>b\))
①\(a\)を\(b\)で割ったときの余りが\(r\)となる。
②(ア)\(r≠0\)のときは、\(b→a\),\(r→b\)として①に戻る。
(イ)\(r=0\)のときは、このときの\(b\)が最大公約数となる。
(例)
\(595\)と\(272\)の最大公約数
\(595\)と\(272\)の最大公約数
(解)
\(595÷272\)を計算して
\(595=\)\(272\)\(×2+\)\(51\) (\(595,272\)の最大公約数=\(272,51\)の最大公約数)
\(595÷272\)を計算して
\(595=\)\(272\)\(×2+\)\(51\) (\(595,272\)の最大公約数=\(272,51\)の最大公約数)
\(272÷51\)を計算して
\(272=\)\(51\)\(×5+\)\(17\) (\(272,51\)の最大公約数=\(51,17\)の最大公約数)
\(51÷17\)を計算して
\(51=\)\(17\)\(×3\) (余り\(0\)なので、\(17\)が最大公約数)
最大公約数は\(17\)
※以上のことを筆算で表すと次のようになります。
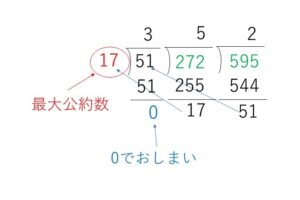
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
ここまで見て頂きありがとうございました。