・\(n\)進法
普段私たちが使う整数は、\(1\)が\(10\)個あつまると\(10\)になり、\(10\)が\(10\)個集まると\(100\)になり・・・と、\(10\)個集まると位が1つ上がる数です。このような\(10\)個あつまると位が1つあがる表し方を十進法といいます。
同じような考え方で、\(1\)が\(n\)個集まると位が1つ上がり、\(n\)が\(n\)個集まる(\(n^2\))と位が1つ上がり、\(n^2\)が\(n\)個集まると位が1つあがり・・・・という\(n\)個集まると位が上がる数の表し方を\(n\)進法といいます。(ただし\(n\)は\(2\)以上の整数とします) また、\(n\)進法で表された数を、\(n\)進数 といいます。
具体的に\(4\)進法を\(10\)進法と比べながら考えてみます。
\(10\)進法について、各\(1,10,10^2,10^3・・・\)の位を部屋にみたてて、コイン1枚を1として考えると、各部屋には\(9\)枚(束)までのコインしか入れず、\(10\)個(束)たまるとそれを束にして、桁数が1つ大きい部屋に移るという仕組みになっています。
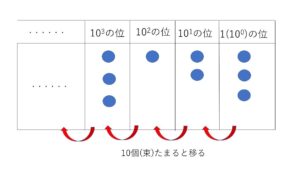
例えば、\(1234\) だと次のような図になり、これを\(1(=10^0),10^1,10^2,10^3\) を使って表すと
\(1234=1×10^3+2×10^2+3×10^1+4×10^0\)
となります。

同様に\(4\)進法について、各\(1,4,4^2,4^3・・・\)の位を部屋にみたてて、コイン1枚を1として考えると、各部屋には\(3\)枚(束)までのコインしか入れず、\(4\)個(束)たまるとそれを束にして、桁数が1つ大きい部屋に移るという仕組みになっています。
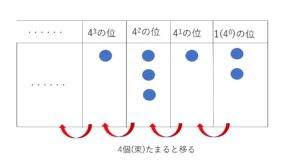
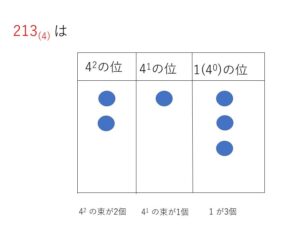
例えば次の図のようなコインの入り方だと、各位の数は順に\(2,1,3\)です。これを左から順に並べた数を、\(4\)進法で表した数\(213_{(4)}\) (右下に\(4\)進法の\(4\)を書く)とします。なお\(213_{(4)}\)を\(10\)進法で表すには、コインの総数を考えればよいので
\(2×4^2+1×4^1+3×4^0=39\)
より、\(39\)となります。
\(39\)枚のコインを\(4\)進法の位上げの法則によって部屋に入れていくと、左から順に\(2,1,3\) となるということです。
これらのことを踏まえると、一般に\(n\)進法では、各位の数は\(0\)から\(n-1\)までの整数となり、\(n\)進法の数 \(a_ka_{k-1}\)\(・・・a_2a_1a_0\)\(_{(n)}\)を\(10\)進法で表すと
\(a_k・n^k+a_{k-1}・n^{k-1}+\)\(・・・+a_1・n^1+a_0・n^0\)
となります。
・\(n\)進法で表された数を\(n\)進数という。
・\(n\)進法の各位の数は\(0\)以上\(n-1\)以下
・\(n\)進法では右下に\(_{(n)}\)と記載する。ただし\(10\)進法では通常省略する。
・\(a_ka_{k-1}\)\(・・・a_2a_1a_0\)\(_{(n)}\)を\(10\)進法で表すと
\(a_k・n^k+a_{k-1}・n^{k-1}+\)\(・・・+a_1・n^1+a_0・n^0\)
なお、\(10\)進法では小数点以下の位は
\(\displaystyle\frac{1}{10}\)の位、\(\displaystyle\frac{1}{10^2}\)の位、\(\displaystyle\frac{1}{10^3}\)の位・・・となり、
同様に\(n\)進法での小数点以下の位は
\(\displaystyle\frac{1}{n}\)の位、\(\displaystyle\frac{1}{n^2}\)の位、\(\displaystyle\frac{1}{n^3}\)の位・・・となります。
では、例題を通して、\(n\)進法で表された数を\(10\)進法で表したり、逆に\(10\)進法で表された数を\(n\)進法で表したりする方法を見ていきます。
ひとまず小数点以下のない整数だけについて考えます。
(例題1)
次の数を\(10\)進法で表せ。
(1)\(101101_{(2)}\)
(2)\(2302_{(5)}\)
(2)では\(5^0,5^1,5^2・・・\)と数字が変わるだけです。
(解答)
(1)
\(101101_{(2)}\)
\(=1・2^5+0・2^4+1・2^3\)\(+1・2^2+0・2^1+1・2^0\)
\(=32+8+4+1\)
\(=\)\(45\)
(2)
\(2302_{(5)}\)
\(=2・5^3+3・5^2+0・5^1+2・5^0\)
\(=250+75+2\)
\(=\)\(327\)
(例題2)
(1)\(10\)進数 \(13\)を\(2\)進法で表せ。
(2)\(10\)進数 \(1000\)を\(9\)進法で表せ。
(解答)
(1)
\(13\)
\(=2×6+1\) (13を2で割る 余り1)
\(=2(2×3+0)+1\) (6を2で割る 余り0)
\(=2^2(2×1+1)+0×2+1\) (3を2で割る 余り1)
\(=1×2^3+1×2^2+0×2+1\) (商が1になったので終わり)
\(=\)\(1101_{(2)}\)
(余りの赤数字が位の数になっている)
以上のことを筆算で書くと
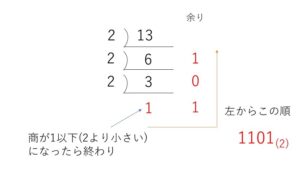
(2)
\(1000\)を\(9\)で割り、商をさらに\(9\)で割り・・・という操作を繰り返す。

余りを順に並べて、\(1331_{(9)}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。