絶対値を含む定積分の問題について見ていきます。
(例題1)
(1)\(\displaystyle\int_{1}^{4}|x^2-2x-3|dx\) の値を求めよ。
(2)\(y=-|x^2-4|+5\), \(y=-|2x|+1\) で囲まれた部分の面積を求めよ。
(解答)
(1)
「\(1≦x≦3\) と \(3≦x≦4\)」 で場合分けします。
定積分が面積を表していることと照らし合わせると分かりやすいと思います。
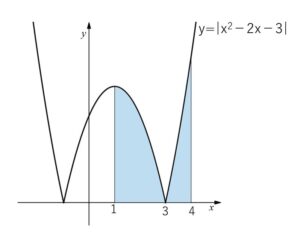
\(y=|x^2-2x-3|=|(x+1)(x-3)|\) より
\(\displaystyle\int_{1}^{4}|x^2-2x-3|dx\)
\(=\displaystyle\int_{1}^{3}-(x^2-2x-3)dx+\displaystyle\int_{3}^{4}(x^2-2x-3)dx\)
\(=-\left[\displaystyle\frac{1}{3}x^3-x^2-3x\right]_{1}^{3}+\left[\displaystyle\frac{1}{3}x^3-x^2-3x\right]_{3}^{4}\)
\(=-(-9+\displaystyle\frac{11}{3})+(-\displaystyle\frac{20}{3}+9)\)
\(=\displaystyle\frac{23}{3}\)
(2)
1つ目の関数は 「\(-2≦x≦2\)」, 「\(x≦-2,x≧2\)」
2つ目の関数は 「\(x≦0\)」, 「\(x≧0\)」
で絶対値が外れるので、\(x≦-2\), \(-2≦x≦0\), \(0≦x≦2\), \(x≧2\) の4パターンになります。
もう少し楽な方法として、グラフの対称性に着目する方法があります。
どちらも、\(x→-x\) としても方程式が変わらないので、\(y\)軸対称です。すると\(x≧0\)だけ考えればよいので、\(0≦x≦2\), \(x≧2\) の2パターンに省略することができます。
\(y=-|x^2-4|+5\), \(y=-|2x|+1\) のグラフはどちらも\(y\)軸について対称だから、\(x≧0\)の部分を考えればよい。
\(y=-|x^2-4|+5\) について
①\(0≦x≦2\) では
\(y=(x^2-4)+5=x^2+1\)
②\(x≧2\) では
\(y=-(x^2-4)+5=-x^2+9\)
\(y=-|2x|+1\) については
\(y=-2x+1\)
②において交点の\(x\)座標を求めると
\(-x^2+9=-2x+1\)
\(x^2-2x-8=0\)
\((x-4)(x+2)=0\)
\(x=4\)
したがってグラフは次の通り。
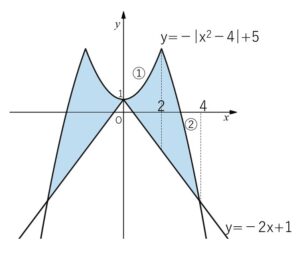
面積を\(S\)とすると
\(\displaystyle\frac{S}{2}=\displaystyle\int_{0}^{2}\{x^2+1-(-2x+1)\}dx+\displaystyle\int_{2}^{4}\{-x^2+9-(-2x+1)\}dx\)
\(=\displaystyle\int_{0}^{2}(x^2+2x)dx+\displaystyle\int_{2}^{4}(-x^2+2x+8)dx\)
\(=\left[\displaystyle\frac{1}{3}x^3+x^2\right]_{0}^{2}+\left[-\displaystyle\frac{1}{3}x^3+x^2+8x\right]_{2}^{4}\)
\(=\displaystyle\frac{20}{3}+(\displaystyle\frac{80}{3}-\displaystyle\frac{52}{3})\)
\(=16\)
したがって
\(S=32\)
(例題2)
\(t\)が区間 \(\left[-\displaystyle\frac{1}{2},2\right]\) を動くとき、
\(F(t)=\displaystyle\int_{0}^{1}x|x-t|dx\) の最大値と最小値を求めよ、
区間 \(\left(-\displaystyle\frac{1}{2},2\right)\) だとイコールなしの区間 \(-\displaystyle\frac{1}{2}<t<2\) になります。
(解答)
積分区間は\(0\)から\(1\)までの一定の区間で、積分変数は\(x\)なので\(x\)で積分すると残るのは\(t\)で、全体としては\(t\)の関数になります。
\(x\)で積分するので、積分する際には\(x\)の関数としてみるから\(t\)は定数扱いです。
あとは絶対値の扱いについて、原則通り中身が正負で場合分けしますが、\(0≦x≦1\) の範囲でグラフを考えればよいので、境目になる\(x=t\)がこの範囲にあるか無いかで場合分けです。
\(F(t)=\displaystyle\int_{0}^{1}x|x-t|dx\) (\(-\displaystyle\frac{1}{2}≦t≦2\))
\(|x-t|\) は
\(x≦t\) のとき \(-(x-t)\)
\(x≧t\) のとき \((x-t)\)
以下 \(0≦x≦1\) の範囲で考えると
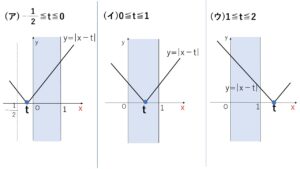
(ア)\(-\displaystyle\frac{1}{2}≦t≦0\) のとき
\(|x-t|=x-t\) より
\(F(t)=\displaystyle\int_{0}^{1}x(x-t)dx\)
\(=\displaystyle\int_{0}^{1}(x^2-tx)dx\)
\(=\left[\displaystyle\frac{1}{3}x^3-\displaystyle\frac{t}{2}x^2\right]_{0}^{1}\)
\(=\displaystyle\frac{1}{3}-\displaystyle\frac{1}{2}t\)
(イ)\(0≦t≦1\) のとき
\(0≦x≦t\) のとき \(|x-t|=-(x-t)\)
\(t≦x≦1\) のとき \(|x-t|=x-t\)
よって
\(F(t)=\displaystyle\int_{0}^{t}-x(x-t)dx+\displaystyle\int_{t}^{1}x(x-t)dx\)
\(=\left[-\displaystyle\frac{1}{3}x^3+\displaystyle\frac{t}{2}x^2\right]_{0}^{t}+\left[\displaystyle\frac{1}{3}x^3-\displaystyle\frac{t}{2}x^2\right]_{t}^{1}\)
\(=(-\displaystyle\frac{1}{3}t^3+\displaystyle\frac{1}{2}t^3)+\{(\displaystyle\frac{1}{3}-\displaystyle\frac{t}{2})-(\displaystyle\frac{1}{3}t^3-\displaystyle\frac{1}{2}t^3)\}\)
\(=\displaystyle\frac{1}{3}t^3-\displaystyle\frac{1}{2}t+\displaystyle\frac{1}{3}\)
(ウ)\(1≦t≦2\) のとき
\(|x-t|=-(x-t)\) より
(ア)において符号を変えればよいので
\(F(t)\)\(=-\displaystyle\frac{1}{3}+\displaystyle\frac{1}{2}t\)
まとめると
\(F(t)=-\displaystyle\frac{1}{2}t+\displaystyle\frac{1}{3}\) (\(-\displaystyle\frac{1}{2}≦t≦0\))
\(F(t)=\displaystyle\frac{1}{3}t^3-\displaystyle\frac{1}{2}t+\displaystyle\frac{1}{3}\) (\(0≦t≦1\))
\(F(t)=\displaystyle\frac{1}{2}t-\displaystyle\frac{1}{3}\) (\(1≦t≦2\))
\(F(t)=\displaystyle\frac{1}{3}t^3-\displaystyle\frac{1}{2}t+\displaystyle\frac{1}{3}\) について
\(F'(t)=t^2-\displaystyle\frac{1}{2}=(t+\displaystyle\frac{1}{\sqrt{2}})(t-\displaystyle\frac{1}{\sqrt{2}})\)
よって増減表は次の通り。
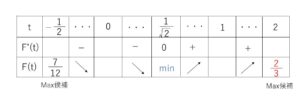
\(F(2)>F(-\displaystyle\frac{1}{2})\) より
最大値 \(F(2)\)\(=\displaystyle\frac{2}{3}\)
最小値 \(F(\displaystyle\frac{1}{\sqrt{2}})\)\(=\displaystyle\frac{1}{3}(\displaystyle\frac{1}{\sqrt{2}})^3-\displaystyle\frac{1}{2}(\displaystyle\frac{1}{\sqrt{2}})+\displaystyle\frac{1}{3}\)\(=\displaystyle\frac{1}{3}-\displaystyle\frac{\sqrt{2}}{6}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→絶対値と積分② back→区間で関数の式が違う積分