引き続き、絶対値に関する積分の問題について見ていきます。
(例題1)
曲線 \(y=x^3-kx\) (\(k\)は定数) を\(C\)、折れ線 \(y=|x|\) を\(C’\)とする。
(1)\(C\)と\(C’\)の共有点の個数を求めよ。
(2)\(C\)と\(C’\)が2個以上の共有点をもつとき、\(C\)と\(C’\)が囲む図形の面積を求めよ。
\(C:y=x^3-kx\) のグラフの特徴をざっくりと考えると、まず原点を通ることはすぐに分かり、あとは「\(x→-x\), \(y→-y\)」としても変わらないことから原点対称です。
(解答)
(1)
\(C’\)は
\(y=x\) \(x≧0\)
\(y=-x\) \(x<0\)
(ア)\(x≧0\)のとき
\(x^3-kx=x\) の実数解の個数を調べると
\(x(x^2-k-1)=0\)・・・① より
(i)\(-k-1>0\) つまり \(k<-1\) のとき
\(x^2-k-1>0\) より 実数解は \(x=0\) のみで1個
(ii)\(-k-1=0\) つまり \(k=-1\) のとき
方程式①は \(x^3=0\) より 実数解は \(x=0\) のみで 1個
(iii)\(-k-1<0\) つまり \(k>-1\) のとき
\(x^2-k-1=0\) の解で\(x≧0\) のものが \(x=\sqrt{k+1}\) でこれは\(0\)でないので
①の実数解の個数は2個
(イ)\(x<0\) のとき
\(x^3-kx=-x\) の実数解の個数を調べると
\(x(x^2-k+1)=0\) より
\(x^2-k+1=0\)・・・② の実数解の個数を調べればよい。
(i)\(-k+1>0\) つまり \(k<1\) のとき
\(x^2-k+1>0\) より ②の実数解の個数は0個
(ii)\(-k+1=0\) つまり \(k=1\) のとき
方程式②は \(x^2=0\) より \(x<0\)を満たす解はなく 0個
(iii)\(-k+1<0\) つまり \(k>1\) のとき
\(x^2-k+1=0\) の解で\(x<0\) のものが \(x=-\sqrt{k-1}\)
②の実数解の個数は1個
(ア)(イ)をまとめると
\(k≦-1\) のとき 1個
\(-1<k≦1\) のとき 2個
\(k>1\) のとき 3個
(2)
(A)については曲線\(C\)が、\(y’=3x^2-k\) より \(k\)の正負で極値が存在するかどうかが変わりますが、共有点の個数は2個のままなので影響はないです。
なお共有点が1個のときは囲む図形は存在しません。
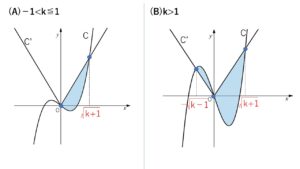
面積を\(S\)とする。
(A)\(-1<k≦1\) のとき
\(S=\displaystyle\int_{0}^{\sqrt{k+1}}\{x-(x^3-kx)\}dx\)
\(=\left[-\displaystyle\frac{1}{4}x^4+\displaystyle\frac{(k+1)}{2}x^2\right]_{0}^{\sqrt{k+1}}\)
\(=-\displaystyle\frac{(k+1)^2}{4}+\displaystyle\frac{(k+1)^2}{2}\)
\(=\displaystyle\frac{(k+1)^2}{4}\)
(B)\(k>1\) のとき
\(S=\displaystyle\int_{-\sqrt{k-1}}^{0}\{x^3-kx-(-x)\}dx+\displaystyle\int_{0}^{\sqrt{k+1}}\{x-(x^3-kx)\}dx\)
(2項目は(A)と同じ)
\(=\left[\displaystyle\frac{1}{4}x^4-\displaystyle\frac{k-1}{2}x^2\right]_{-\sqrt{k-1}}^{0}+\displaystyle\frac{(k+1)^2}{4}\)
\(=-\left\{\displaystyle\frac{(k-1)^2}{4}-\displaystyle\frac{(k-1)^2}{2}\right\}+\displaystyle\frac{(k+1)^2}{4}\)
\(=\displaystyle\frac{(k-1)^2}{4}+\displaystyle\frac{(k+1)^2}{4}\)
\(=\displaystyle\frac{k^2+1}{2}\)
(例題2)
関数 \(f(x)\) が
\(f(x)=x^2-x\displaystyle\int_{0}^{2}|f(t)|dt\)
を満たしているとする、このとき \(f(x)\) を求めよ。
よって \(\displaystyle\int_{0}^{2}|f(t)|dt=k\) として処理できます。しかも絶対値がついた関数の積分なので\(0\)以上の値になります。
(解答)
\(\displaystyle\int_{0}^{2}|f(t)|dt=k\)・・・① (\(k\)は定数、\(k≧0\)) とおけて
\(f(x)=x^2-kx=x(x-k)\)・・・②
②を①に代入すると
\(\displaystyle\int_{0}^{2}|t(t-k)|dt=k\)
下に凸の2次関数 \(y=t(t-k)\) の\(t\)軸との交点は \(t=0,k\) で、積分区間が \(0≦t≦2\) なので、\(k\)がこの区間にあるかないかで場合分けします。
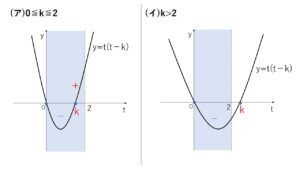
(ア)\(0≦k≦2\) のとき
\(\displaystyle\int_{0}^{2}|t(t-k)|dt\)
\(=\displaystyle\int_{0}^{k}-t(t-k)dt+\displaystyle\int_{k}^{2}t(t-k)dt\)
\(=\left[-\displaystyle\frac{1}{3}t^3+\displaystyle\frac{k}{2}t^2\right]_{0}^{k}+\left[\displaystyle\frac{1}{3}t^3-\displaystyle\frac{k}{2}t^2\right]_{k}^{2}\)
\(=\displaystyle\frac{1}{6}k^3+(\displaystyle\frac{8}{3}-2k)-(-\displaystyle\frac{1}{6}k^3)\)
\(=\displaystyle\frac{1}{3}k^3-2k+\displaystyle\frac{8}{3}\)
よって
\(\displaystyle\frac{1}{3}k^3-2k+\displaystyle\frac{8}{3}=k\) より
\(k^3-9k+8=0\)
\((k-1)(k^2+k-8)=0\)
\(k=1,\displaystyle\frac{-1±\sqrt{33}}{2}\)
\(0≦k≦2\) を満たすのは
\(k=1\)
(イ)\(k>2\) のとき
\(\displaystyle\int_{0}^{2}|t(t-k)|dt\)
\(=\displaystyle\int_{0}^{2}-t(t-k)dt\)
\(=\left[-\displaystyle\frac{1}{3}t^3+\displaystyle\frac{k}{2}t^2\right]_{0}^{2}\)
\(=-\displaystyle\frac{8}{3}+2k\)
よって
\(-\displaystyle\frac{8}{3}+2k=k\) より
\(k=\displaystyle\frac{8}{3}\)(\(k>2\)を満たす)
②より
\(f(x)=x^2-x\) または \(f(x)=x^2-\displaystyle\frac{8}{3}x\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→区間 [a,a+1] の積分 back→絶対値と積分①