積分区間が \([a,a+1]\) となっている定積分の問題について見ていきます。
(例題1)
関数 \(g(x)=\displaystyle\int_{x}^{x+1}|t(t-3)|dt\) の \(0≦x≦3\) における最大値を求めよ。また、そのときの\(x\)の値を求めよ。
積分区間は \(x≦t≦x+1\) で、\(x\)の値によって変化します。ただし区間の幅は\(1\)で固定されています。したがって積分する区間が幅1のまま左右に動くイメージです。
(解答)
(i)\(x+1≦3\) (ii)\(x+1>3\) で場合分けです。
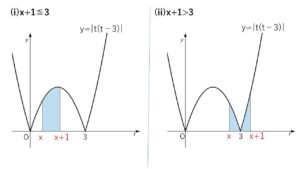
\(0≦x≦3\) だから
(i)\(x+1≦3\) つまり \(0≦x≦2\) のとき
\(g(x)=\displaystyle\int_{x}^{x+1}|t(t-3)|dt\)
\(=\displaystyle\int_{x}^{x+1}-t(t-3)dt\)
\(=\left[-\displaystyle\frac{1}{3}t^3+\displaystyle\frac{3}{2}t^2\right]_{x}^{x+1}\)
\(=-\displaystyle\frac{1}{3}(x+1)^3+\displaystyle\frac{3}{2}(x+1)^2-\{-\displaystyle\frac{1}{3}x^3+\displaystyle\frac{3}{2}x^2\}\)
\(=-x^2+2x+\displaystyle\frac{7}{6}\)
(ii)\(x+1>3\) つまり \(2<x≦3\) のとき
\(g(x)=\displaystyle\int_{x}^{x+1}|t(t-3)|dt\)
\(=\displaystyle\int_{x}^{3}-t(t-3)dt+\displaystyle\int_{3}^{x+1}t(t-3)dt\)
\(=\left[-\displaystyle\frac{1}{3}t^3+\displaystyle\frac{3}{2}t^2\right]_{x}^{3}+\left[\displaystyle\frac{1}{3}t^3-\displaystyle\frac{3}{2}t^2\right]_{3}^{x+1}\)
\(=\left\{-9+\displaystyle\frac{27}{2}-(-\displaystyle\frac{1}{3}x^3+\displaystyle\frac{3}{2}x^2)\right\}+\left\{\displaystyle\frac{1}{3}(x+1)^3-\displaystyle\frac{3}{2}(x+1)^2-(9-\displaystyle\frac{27}{2})\right\}\)
\(=\displaystyle\frac{2}{3}x^3-2x^2-2x+\displaystyle\frac{47}{6}\)
\(0≦x≦2\) のとき
\(g(x)=-(x-1)^2+\displaystyle\frac{13}{6}\)
\(2<x≦3\) のとき
\(g'(x)=2x^2-4x-2=2(x^2-2x-1)\)
\(x^2-2x-1=0\) を満たすのは \(x=1+\sqrt{2}\)
よって増減表は次の通り。
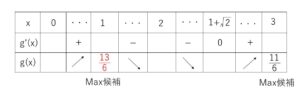
\(g(3)=18-18-6+\displaystyle\frac{47}{6}=\displaystyle\frac{11}{6}<g(1)\) より
最大値は \(x=1\) のとき \(\displaystyle\frac{13}{6}\)
(例題2)
(1)\(a\)を正の数とする。区間 \([a,a+1]\) において、放物線 \(y=x^2-1\) と \(x\)軸とではさまれる部分の面積\(S\)を求めよ。
(2)\(S\)を最小にする\(a\)の値を求めよ。
\(a\)は正の数なので、区間の左端は\(0~\),区間の右端は\(1~\)を動くので、 境目\(x=1\)に着目して
(i)\(0<a≦1\) (ii)\(a>1\) で場合分けします。
(1)
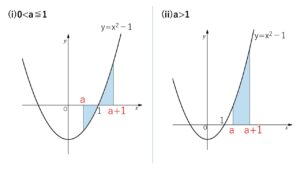
(i)\(0<a≦1\) のとき
\(S=\displaystyle\int_{a}^{1}(-x^2+1)dx+\displaystyle\int_{1}^{a+1}(x^2-1)dx\)
\(=\left[-\displaystyle\frac{1}{3}x^3+x\right]_{a}^{1}+\left[\displaystyle\frac{1}{3}x^3-x\right]_{1}^{a+1}\)
\(=\left\{\displaystyle\frac{2}{3}-(-\displaystyle\frac{1}{3}a^3+a)\right\}+\left\{\displaystyle\frac{1}{3}(a+1)^3-(a+1)-(-\displaystyle\frac{2}{3})\right\}\)
\(=\displaystyle\frac{2}{3}a^3+a^2-a+\displaystyle\frac{2}{3}\)
(ii)\(a>1\) のとき
\(S=\displaystyle\int_{a}^{a+1}(x^2-1)dx\)
\(=\left[\displaystyle\frac{1}{3}x^3-x\right]_{a}^{a+1}\)
\(=\displaystyle\frac{1}{3}(a+1)^3-(a+1)-\left(\displaystyle\frac{1}{3}a^3-a\right)\)
\(=a^2+a-\displaystyle\frac{2}{3}\)
答
\(S=\displaystyle\frac{2}{3}a^3+a^2-a+\displaystyle\frac{2}{3}\) (\(0<a≦1\))
\(S=a^2+a-\displaystyle\frac{2}{3}\) (\(a>1\))
(2)
\(0<a≦1\) のとき
\(S’=2a^2+2a-1\)
\(S’=0\) となるのは
\(a=\displaystyle\frac{-1±\sqrt{3}}{2}\) の大きい方
\(a>1\) のとき
\(S’=2a+1>0\)
したがって増減表は次の通り。
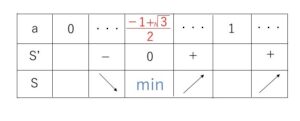
最小となる\(a\)は
\(a=\displaystyle\frac{-1+\sqrt{3}}{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→y軸方向の積分 back→絶対値と積分②