曲線と\(y\)軸の間の部分の図形の面積について見ていきます。
・\(y\)軸方向の積分と面積
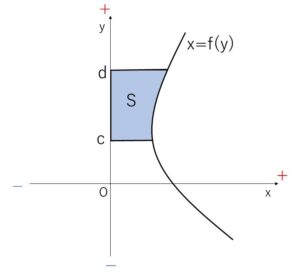
\(y\)の関数 \(x=f(y)\) が、区間 \(c≦y≦d\) で \(f(y)≧0\) とする。
曲線 \(x=f(y)\) と 「\(y\)軸, 2直線 \(y=c\), \(y=d\)」 で囲まれた図形の面積は次の定積分で表されます。
\(S=\displaystyle\int_{c}^{d}f(y)dy\)
注意することは、\(x\)を\(y\)の関数で表して(\(x=(yの式)\)の形にする)、\(y\)で積分することと、軸の正の方向が「\(y\)については上方向、\(x\)については右方向」になっていることです。
また、負の領域の面積、2曲線で囲まれた面積についても、\(x\)での積分のときと同じことが成り立ちます。他にも1/6公式など\(x\)の積分について成り立ったことは、\(y\)の積分についても基本的には成り立ちます。
(例題1)
(1)曲線 \(x=y^2+2\) と \(y\)軸 と 2直線 \(y=-1\), \(y=2\) で囲まれた部分の面積を求めよ。
(2)曲線 \(y^2=2x+5\), 直線 \(y=x+1\) で囲まれた部分の面積を求めよ。
(解答)
(1)
曲線 \(x=f(y)=y^2+2\) は2次関数なので放物線になり、軸は \(y=0\) です。ちょうど\(x\)の2次関数を横に倒した形になります。
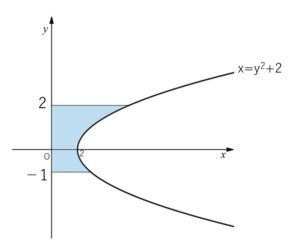
面積\(S\)は
\(S=\displaystyle\int_{-1}^{2}(y^2+2)dy\)
\(=\left[\displaystyle\frac{1}{3}y^3+2y\right]_{-1}^{2}\)
\(=(\displaystyle\frac{8}{3}+4)-(-\displaystyle\frac{1}{3}-2)\)
\(=9\)
(2)
曲線 \(x=\displaystyle\frac{1}{2}y^2-\displaystyle\frac{5}{2}\), 直線 \(x=y-1\)
となりますが、直線のグラフについては \(y=x+1\) のままで考えた方が分かりやすいと思います。
曲線(放物線)と直線の囲む面積なので、1/6公式が使える形です。2つの方程式を連立して交点の\(y\)座標を求めていきます。
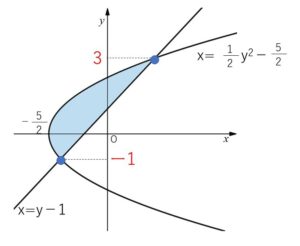
曲線と直線の方程式より
\(x=\displaystyle\frac{1}{2}y^2-\displaystyle\frac{5}{2}\)・・・①
\(x=y-1\)・・・②
①②より\(x\)を消去して
\(\displaystyle\frac{1}{2}y^2-\displaystyle\frac{5}{2}=y-1\)
\(\displaystyle\frac{1}{2}(y^2-2y-3)=0\)
\(\displaystyle\frac{1}{2}(y+1)(y-3)=0\)
\(y=-1,3\) (交点の\(y\)座標)
よって面積\(S\)は
\(S=\displaystyle\int_{-1}^{3}\{y-1-(\displaystyle\frac{1}{2}y^2-\displaystyle\frac{5}{2})\}dy\)
\(=-\displaystyle\frac{1}{2}\displaystyle\int_{-1}^{3}(y+1)(y-3)dy\)
\(=-\displaystyle\frac{1}{2}\cdot(-\displaystyle\frac{1}{6})(3+1)^3\)
\(=\displaystyle\frac{16}{3}\)
(例題2)
\(xy\)平面上の曲線
\(C_1:y=x-x^2\) および \(C_2:x=y-y^2\)
について
(1)\(C_1\)の \(x=t\) における接線の方程式を求めよ。
(2) (1)で求めた接線が\(C_2\)にも接するときの\(t\)の値と接線の方程式を求めよ。
(3) (2)で求めたすべての接線と曲線\(C_2\)で囲まれる図形の面積を求めよ。
\(C_1,C_2\)は\(x,y\)を入れ替えた関係なので、\(y=x\)について対称です。
\(C_1,C_2\)の細かい位置関係(交点の個数など) については、本問ではそこまで正確に調べる必要はありませんが、気になる方は解答の後に詳細を書いておくのでそちらを見てください。
(解答)
(1)
\(C_1:y=x-x^2\) において
\(y’=1-2x\)
よって\(x=t\)における接線の方程式は
\(y=(1-2t)(x-t)+t-t^2\)
整理して
\(y=(1-2t)x+t^2\)・・・①
(2)
整式だと問題なく「接する=重解」が使えるので、(1)で求めた①より\(x\)を消去して、\(y\)の方程式が重解をもつ条件を考えます。
(\(y\)消去で\(x\)の方程式にするよりこちらのほうが無難だと思います。)
①より
\((1-2t)x=y-t^2\)・・・②
ここで \(t=\displaystyle\frac{1}{2}\) とすると、①は \(y=\displaystyle\frac{1}{4}\) となるが、\(y=\displaystyle\frac{1}{4}\) (\(x\)軸に平行な直線) は \(C_2:x=y-y^2\) には接しないので、\(t≠\displaystyle\frac{1}{2}\) としてよい。
②より
\(x=\displaystyle\frac{y-t^2}{1-2t}\) を\(C_2\)の方程式に代入して
\(\displaystyle\frac{y-t^2}{1-2t}=y-y^2\)
整理すると
\((1-2t)y^2+2ty-t^2=0\)・・・③
この\(y\)の方程式が重解をもてばよいので
\(\displaystyle\frac{D}{4}=0\)
\(t^2+(1-2t)t^2=0\)
\(t^2(2-2t)=0\)
\(t=0,1\)
接線の方程式は①より
\(y=x\) (\(t=0\))
\(y=-x+1\) (\(t=1\))
(3)
解答では\(C_2\)の接点の座標を、(2)で求めた接線の方程式から計算していきます。
(\(C_2\)の接点の\(y\)座標は③の重解になっていることを利用してもよいし、\(C_1,C_2\)の対称性から考えてもよい)
また、\(C_2\)は\(y\)の整式なので、\(y\)軸方向に積分します。
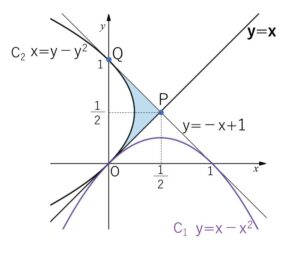
\(y=x\)・・・④
\(y=-x+1\)・・・⑤
\(x=y-y^2\)・・・⑥
④⑤の交点\(P\)の座標は\((\displaystyle\frac{1}{2},\displaystyle\frac{1}{2})\)
④⑥の交点の\(y\)座標は
\(y=y-y^2\)
\(y^2=0\)
\(y=0\)
このとき \(x=0\) (交点は原点\(O\))
⑤⑥の交点の\(y\)座標は
\(-y+1=y-y^2\)
\(y^2-2y+1=0\)
\((y-1)^2=0\)
\(y=1\)
このとき \(x=0\) (この交点を\(Q\)とする)
したがって面積\(S\)は
\(S=△OPQ-\displaystyle\int_{0}^{1}(y-y^2)dy\)
\(=\displaystyle\frac{1}{2}\cdot1\cdot\displaystyle\frac{1}{2}-\left[\displaystyle\frac{1}{2}y^2-\displaystyle\frac{1}{3}y^3\right]_{0}^{1}\)
\(=\displaystyle\frac{1}{4}-\displaystyle\frac{1}{6}\)
\(=\displaystyle\frac{1}{12}\)
※\(C_1,C_2\)の位置関係について
対称軸\(y=x\)がちょうど\(C_1,C_2\)の接線になっていて、
\(C_1\)は接点以外は\(y=x\)より右側にあることから、\(C_2\)も接点以外は\(y=x\)より左側にあるので、\(C_1,C_2\)の交点はこの接点(原点)以外には無いことになります。
もしくは、\(y=x-x^2\)・・・(i) を \(x=y-y^2\)・・・(ii) に代入して
\(x=x-x^2-(x-x^2)^2\)
整理すると
\(x^4-2x^3+2x^2=0\)
\(x^2(x^2-2x+2)=0\)
\(x^2-2x+2=0\) の解は虚数なので、\(x=0\)のみが実数解になり、(i),(ii)を同時に満たす\(y\)は \(y=0\) だから、原点のみが交点になることが分かります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→対称な図形の面積 back→区間 [a,a+1] の積分