対称性のある図形の面積を求める問題について見ていきます。
(例題1)
曲線 \(y=x^3-3x^2+3x\) のグラフを\(C\)とする。直線 \(y=x\) に関して\(C\)と対称なグラフを\(C’\)とする。このとき\(C\)と\(C’\)で囲まれた図形の面積を求めよ。
そこで、\(C,C’\)と\(y=x\)を対称性に着目して図示して、\(y=x\) と \(C\) の囲む面積を考えます。するとちょうどこの面積の2倍が\(C,C’\)の囲む面積になっていることが分かります。
なお積分する際には \(y=x\) と \(C\) の上下関係には気を付けておきます。
(解答)
\(C\)と\(y=x\)の交点を求めると
\(x=x^3-3x^2+3x\) より
\(x^3-3x^2+2x=0\)
\(x(x-1)(x-2)=0\)
\(x=0,1,2\)
したがって曲線\(C\), \(y=x\) と、曲線\(C’\)(\(C\)と対称) を図示すると次の通り。
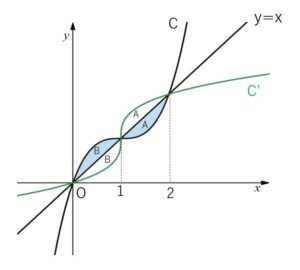
図の\(A\)どうし,\(B\)どうしの図形の面積は等しいので、\(C,C’\)の囲む面積を\(S\)とすると
\(\displaystyle\frac{S}{2}=A+B\)
\(=\displaystyle\int_{0}^{1}\{(x^3-3x^2+3x)-x\}dx+\displaystyle\int_{1}^{2}\{x-(x^3-3x^2+3x)\}dx\)
\(=\displaystyle\int_{0}^{1}(x^3-3x^2+2x)dx+\displaystyle\int_{1}^{2}(-x^3+3x^2-2x)dx\)
\(=\left[\displaystyle\frac{1}{4}x^4-x^3+x^2\right]_{0}^{1}+\left[-\displaystyle\frac{1}{4}x^4+x^3-x^2\right]_{1}^{2}\)
\(=\displaystyle\frac{1}{4}+\displaystyle\frac{1}{4}\)
\(=\displaystyle\frac{1}{2}\)
よって
\(S=1\)
(例題2)
\(f(x)=x^3-x\) とし、\(t\)を実数とする。\(xy\)平面において、曲線 \(y=f(x)\) を\(C_1\)とし、直線 \(x=t\) に関して \(C_1\) と対称な曲線 \(y=f(2t-x)\) を\(C_2\)とする。
(1)\(C_1\)と\(C_2\)が3点で交わるとき、\(t\)のとりうる値の範囲を求めよ。
(2)\(t\)が(1)で求めた範囲を動くとき、\(C_1\)と\(C_2\)で囲まれた部分の面積\(S\)の最大値を求めよ。
(解答)
(1)
\(y=f(x)=x^3-x\)・・・①
\(y=f(2t-x)=(2t-x)^3-(2t-x)\)・・・②
①②より\(y\)を消去して
\(x^3-x=(2t-x)^3-(2t-x)\)
展開して\(x\)について整理すると
\(2x^3-6tx^2+(12t^2-2)x-8t^3+2t=0\)
\(2\{x^3-3tx^2+(6t^2-1)x-4t^3+t\}=0\)
\(2(x-t)(x^2-2tx+4t^2-1)=0\)・・・③
\(x\)の方程式③が異なる3つの実数解をもてば3点で交わる。
③の1つの解は \(x=t\) だから、
\(x^2-2tx+4t^2-1=0\)・・・④ が \(x=t\) ではない異なる2つの実数解をもてばよい。
④で\(x=t\) とすると
\(t^2-2t^2+4t^2-1=0\)
\(t=±\displaystyle\frac{1}{\sqrt{3}}\)
よって
\(t≠±\displaystyle\frac{1}{\sqrt{3}}\)
④の判別式ついて \(\displaystyle\frac{D}{4}>0\) より
\(t^2-(4t^2-1)>0\)
\(3t^2-1<0\)
\(-\displaystyle\frac{1}{\sqrt{3}}<t<\displaystyle\frac{1}{\sqrt{3}}\)
したがって異なる3点で交わる\(t\)のとりうる値の範囲は
\(-\displaystyle\frac{1}{\sqrt{3}}<t<\displaystyle\frac{1}{\sqrt{3}}\)
(2)
積分計算はまともにやると大変なので工夫します。
まず、交点の\(t\)以外の\(x\)座標をとりあえず\(x=α,β\) とおいて(計算では\(α,β\)の一方しか使わない)、最後に代入します。積分計算も \((x-t)\)という形を作るようにして、下端 or 上端 の一方の代入が楽になるようにします。
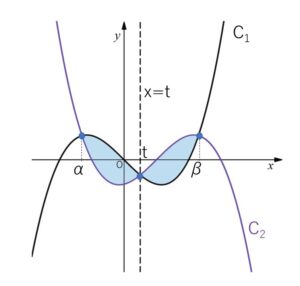
\(C_1,C_2\)で囲まれた図形は\(x=t\)について対称。
2曲線の\(x=t\)以外の交点の\(x\)座標を\(α,β\) (\(α<β\))とすると(1)より
\(x^2-2tx+4t^2-1=0\) の2解が\(α,β\) になるので
\(α=t-\sqrt{1-3t^2}\), \(β=t+\sqrt{1-3t^2}\)
よって
\(S=2\displaystyle\int_{t}^{β}\{f(2t-x)-f(x)\}dx\)
(被積分関数は③の左辺の符号を反対にしたものになるから)
\(=-4\displaystyle\int_{t}^{β}(x-t)(x^2-2tx+4t^2-1)dx\)
\(=-4\displaystyle\int_{t}^{β}(x-t)\{(x-t)^2+3t^2-1\}dx\)
\(=-4\displaystyle\int_{t}^{β}\{(x-t)^3+(3t^2-1)(x-t)\}dx\)
\(=-4\left[\displaystyle\frac{(x-t)^4}{4}+(3t^2-1)\cdot\displaystyle\frac{(x-t)^2}{2}\right]_{t}^{β}\)
\(=-(β-t)^4-2(3t^2-1)(β-t)^2\)
\(β=t+\sqrt{1-3t^2}\) を代入して
\(S=-(\sqrt{1-3t^2})^4-2(3t^2-1)(\sqrt{1-3t^2})^2\)
\(=-(1-3t^2)^2+2(1-3t^2)^2\)
\(=(1-3t^2)^2\)
\(t=0\) と 端点 \(t=±\displaystyle\frac{1}{\sqrt{3}}\) のときの値を考えます。
(1)より \(-\displaystyle\frac{1}{\sqrt{3}}<t<\displaystyle\frac{1}{\sqrt{3}}\) だから
\(0<1-3t^2≦1\)
したがって\(S\)の最大値は \(1^2=1\)
答 \(S\)の最大値 \(1\) (\(t=0\))
※\(x=t\)に関して \(y=f(x)\) と対称な曲線の方程式の求め方
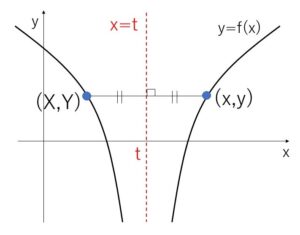
\(y=f(x)\) 上の点を \((x,y)\), この点に対称な点を \((X,Y)\) とおく。
\(\displaystyle\frac{x+X}{2}=t\)・・・(i)
\(y=Y\)・・・(ii)
(i)より \(x=2t-X\)・・・(iii)
(ii),(iii) を \(y=f(x)\) に代入して
\(Y=f(2t-X)\)
\((X,Y)\) は、\(y=f(x)\) 上の点に対称な点の集まりだから、求める方程式は \(X→x\), \(Y→y\) と直すと
\(y=f(2t-x)\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→軌跡・領域と面積 back→y軸方向の積分