円と曲線に囲まれた面積

円と曲線に囲まれた面積を求める例題です。

(例題1)
放物線 \(C:\ y=x^2\) がある。\(y\)軸上に中心をもつ半径\(1\)の円\(K\)が、\(C\)と異なる2点で接線を共有している(2点で接している)。

(1)円\(K\)の中心の座標を求めよ。
(2)\(C\)と\(K\)とで囲まれた図形の面積を求めよ。

(解答)
(1)

(解答1)重解を利用

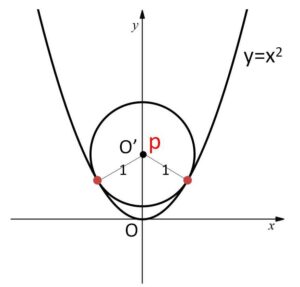
円の中心の座標を \(O'(0,p)\) とおくと円の方程式は
\(x^2+(y-p)^2=1\)・・・①

放物線の方程式は
\(y=x^2\)・・・②

②を①に代入して\(x\)を消去すると
\(y+(y-p)^2=1\)
整理して
\(y^2-(2p-1)y+p^2-1=0\)・・・③

②より \(y≧0\) で、異なる2点で接するので、③が正の重解をもてばよく (\(y=0\) の重解をもつと異なる2点で接しない)
\(D=0\)
\((2p-1)^2-4(p^2-1)=0\)
\(-4p+5=0\)
\(p=\displaystyle\frac{5}{4}\)

このとき③の重解は
\(y=\displaystyle\frac{2p-1}{2}=\color{blue}{\displaystyle\frac{3}{4}}>0\)
となり、正の重解となる。

よって円の中心の座標は
\((0,\displaystyle\frac{5}{4})\)

(解答2)法線を利用

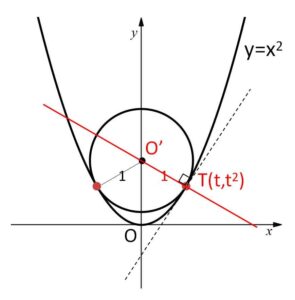
接点を \(T(t,t^2)\) とおくと
\(T\)における接線の傾きは \(y’=2x\) より \(2t\)
原点で接するときは、2点で接することはないので、\(t≠0\)

よって\(T\)における法線の方程式は
\(y=-\displaystyle\frac{1}{2t}(x-t)+t^2\)
整理すると
\(y=-\displaystyle\frac{1}{2t}x+(t^2+\displaystyle\frac{1}{2})\)
この直線の\(y\)切片が円の中心\(O’\)となるから
\(O'(0,t^2+\displaystyle\frac{1}{2})\)

また \(O’T=1\) より
\(\sqrt{t^2+(\displaystyle\frac{1}{2})^2}=1\)
\(t^2+\displaystyle\frac{1}{4}=1\)
ゆえに
\(t^2=\displaystyle\frac{3}{4}\)

したがって円の中心\(O’\)の座標は
\((0,\displaystyle\frac{5}{4})\)

(2)

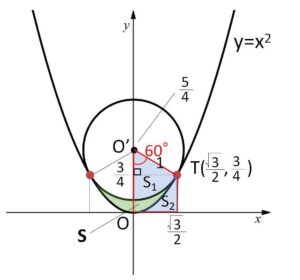
対称性より右半分を考える。

(解答1)より、③の重解は \(y=\displaystyle\frac{3}{4}\)
放物線 \(y=x^2\) に代入して
\(x=±\displaystyle\frac{\sqrt{3}}{2}\)
よって、接点のうち第1象限にあるもの\(T\)の座標は
\(T(\displaystyle\frac{\sqrt{3}}{2},\displaystyle\frac{3}{4})\)

また、辺の比が \(1:2:\sqrt{3}\) の直角三角形の1角が\(60°\)であることから
\(\angle TO’O=60°\)

ゆえに求める面積を\(S\)とすると、台形から扇形\(S_1\)、放物線と\(x\)軸との間の図形\(S_2\)を除くことを考えて
\(\displaystyle\frac{S}{2}=\displaystyle\frac{1}{2}(\displaystyle\frac{3}{4}+\displaystyle\frac{5}{4})\cdot\displaystyle\frac{\sqrt{3}}{2}-1^2\cdotπ\cdot\displaystyle\frac{60}{360}-\displaystyle\int_{0}^{\frac{\sqrt{3}}{2}}x^2dx\)

\(=\displaystyle\frac{\sqrt{3}}{2}-\displaystyle\frac{π}{6}-\displaystyle\frac{1}{3}\cdot(\displaystyle\frac{\sqrt{3}}{2})^3\)

\(=\displaystyle\frac{3\sqrt{3}}{8}-\displaystyle\frac{π}{6}\)

したがって
\(S=\displaystyle\frac{3\sqrt{3}}{4}-\displaystyle\frac{π}{3}\)

(例題2)
円\(C\)は放物線 \(y=x^2\) と点 \(A(\displaystyle\frac{\sqrt{3}}{2},\displaystyle\frac{3}{4})\) において共通の接線をもち、さらに\(x\)軸と\(x>0\)の部分で接している。

(1)円\(C\)の中心\(B\)の座標を求めよ。
(2)円\(C\)、放物線\(P\)と\(x\)軸とによって囲まれて、円\(C\)の外部にある部分の面積\(S\)を求めよ。

(解答)
(1)

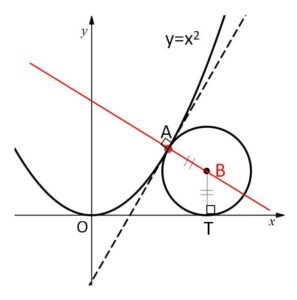
\(y’=2x\) より、\(A(\displaystyle\frac{\sqrt{3}}{2},\displaystyle\frac{3}{4})\) における接線の傾きは\(\sqrt{3}\)。
よって\(A\)における法線の方程式は
\(y=-\displaystyle\frac{1}{\sqrt{3}}(x-\displaystyle\frac{\sqrt{3}}{2})+\displaystyle\frac{3}{4}\)
\(y=-\displaystyle\frac{1}{\sqrt{3}}x+\displaystyle\frac{5}{4}\)
この法線は円の中心\(B\)を通るから
\(B(t,-\displaystyle\frac{1}{\sqrt{3}}t+\displaystyle\frac{5}{4})\)
とおける。

円と\(x\)軸との接点を\(T\)とおけば
\(AB=BT\) より
\(\sqrt{(t-\displaystyle\frac{\sqrt{3}}{2})^2+(-\displaystyle\frac{1}{\sqrt{3}}t+\displaystyle\frac{1}{2})^2}=\left|-\displaystyle\frac{1}{\sqrt{3}}t+\displaystyle\frac{5}{4}\right|\)

\((t-\displaystyle\frac{\sqrt{3}}{2})^2+(-\displaystyle\frac{1}{\sqrt{3}}t+\displaystyle\frac{1}{2})^2=(-\displaystyle\frac{1}{\sqrt{3}}t+\displaystyle\frac{5}{4})^2\)

整理して
\(t^2-\displaystyle\frac{\sqrt{3}}{2}t-\displaystyle\frac{9}{16}=0\)

\((t-\displaystyle\frac{3\sqrt{3}}{4})(t+\displaystyle\frac{\sqrt{3}}{4})=0\)

ここで、円は\(x\)軸の正の部分で接するので\(t>0\)だから
\(t=\displaystyle\frac{3\sqrt{3}}{4}\)

したがって円の中心\(B\)の座標は
\(B(\displaystyle\frac{3\sqrt{3}}{4},\displaystyle\frac{1}{2})\)

(2)

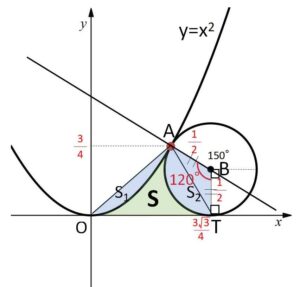
法線\(AB\)の傾きは(1)より\(-\displaystyle\frac{1}{\sqrt{3}}\)だから
\(\angle ABT=360°-(150°+90°)=120°\)

四角形\(OABT\)\(=△OAT+△ABT\)
\(=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{3\sqrt{3}}{4}\cdot\displaystyle\frac{3}{4}+\displaystyle\frac{1}{2}\cdot(\displaystyle\frac{1}{2})^2\sin120°\)
\(=\displaystyle\frac{11\sqrt{3}}{32}\)

図の\(S_1\)について、直線\(OA\)の方程式を \(y=l(x)\) とおくと、\(A\)の\(x\)座標は\(\displaystyle\frac{\sqrt{3}}{2}\) だから
\(S_1=\displaystyle\int_{0}^{\frac{\sqrt{3}}{2}}(l(x)-x^2)dx\)
\(=\displaystyle\frac{1}{6}(\displaystyle\frac{\sqrt{3}}{2}-0)^3\)
\(=\displaystyle\frac{\sqrt{3}}{16}\)

扇形\(S_2\)について
\(S_2=π(\displaystyle\frac{1}{2})^2\cdot\displaystyle\frac{120}{360}=\displaystyle\frac{π}{12}\)

したがって
\(S=(四角形OABT)-(S_1+S_2)\)
\(=\displaystyle\frac{11\sqrt{3}}{32}-(\displaystyle\frac{\sqrt{3}}{16}+\displaystyle\frac{π}{12})\)
\(=\displaystyle\frac{9\sqrt{3}}{32}-\displaystyle\frac{π}{12}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→定積分と体積の関係　back→軌跡・領域と面積