定積分と面積に関するやや発展的な問題について見ていきます。
(例題1)
\(a\)を正の数とする。\(xy\)平面において、次の条件(A),(B)を満たす直線\(l\)が存在するような\(a\)の値の範囲を求めよ。
(A)\(l\)の\(y\)切片は\(a\)である。
(B)放物線 \(y=3x^2\) と \(l\) で囲まれる図形の面積は\(4\)以下である。
(B)は1/6公式を利用します。面積計算で必要な解の差は、解の公式,解と係数の関係どちらを使ってもよいです。
(解答)
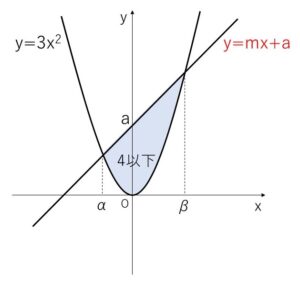
直線\(l\)の傾きを\(m\)とすれば
\(l:y=mx+a\)
放物線と直線の方程式から\(y\)を消去して
\(3x^2=mx+a\)
\(3x^2-mx-a=0\)・・・①
①の判別式
\(D=m^2+12a>0\) (∵\(a>0\))
より①は異なる2つの実数解をもち、それらを\(α,β\) (\(α<β\)) とおくと交点の\(x\)座標であり、解と係数の関係から
\(α+β=\displaystyle\frac{m}{3}\)
\(αβ=-\displaystyle\frac{a}{3}\)
図形の面積\(S\)は
\(S=\displaystyle\int_α^β(mx+a-3x^2)dx\)
\(=\displaystyle\int_α^β-3(x-α)(x-β)dx\)
\(=\displaystyle\frac{1}{2}(β-α)^3\)
\(S≦4\) より
\(\displaystyle\frac{1}{2}(β-α)^3≦4\)
\((β-α)^3≦8\)
\(β-α≦2\)・・・②
ここで
\((β-α)^2=α^2+β^2-2αβ\)
\(=(α+β)^2-4αβ\)
\(=\displaystyle\frac{m^2}{9}+\displaystyle\frac{4a}{3}\)
②より
\((β-α)^2≦4\) だから
\(\displaystyle\frac{m^2}{9}+\displaystyle\frac{4a}{3}≦4\)
\(m^2≦36-12a\)・・・③
ここで直線\(l\)が存在するということは、③を満たすような\(m\)(実数)が存在する(1つでもあればよい)ということであり、③の右辺が正の数、例えば\(a=1\) のときは \(m^2≦24\) となり、これを満たす\(m\)は複数あるので条件に適しますが(これらの\(m\)全部で面積が4以下になる)、\(a=4\) とすると、\(m^2≦-12\) となり(右辺が負の数)、これを満たす実数\(m\)は存在しないので直線\(l\)も存在しないことになります。
また、\(m^2=0\) のときは \(m=0\) がとれるのでOKです。
したがって直線\(l\)が存在する、つまり実数\(m\)が存在する条件は、\(36-12a≧0\) です。
③を満たす実数\(m\)が存在すれば条件を満たす直線\(l\)が存在するので
\(36-12a≧0\)
\(a≦3\)
\(a>0\)とあわせて
\(0<a≦3\)
(例題2)
平面上に、放物線 \(y=x^2-5x+6\) と 直線 \(y=kax-a^2-5a\) がある。
(1)すべての実数\(a\)に対して放物線と直線が異なる2点で交わるような定数\(k\)の値の範囲を求めよ。
(2) (1)で求めた範囲にあって、放物線と直線で囲まれる部分の面積が\(a\)の値によらず一定になるような定数\(k\)の値を求めよ。
(解答)
(1)
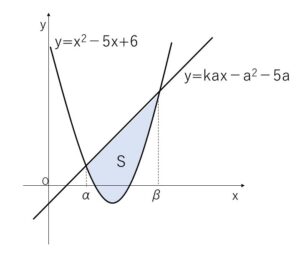
\(x^2-5x+6=kax-a^2-5a\)
\(x\)について整理して
\(x^2-(ka+5)x+a^2+5a+6=0\)・・・(i)
この\(x\)の2次方程式(i)が2つの異なる実数解をもつとき、放物線と曲線が異なる2点で交わるから
\((ka+5)^2-4(a^2+5a+6)>0\)
よって\(a\)について整理します。
\(a\)について整理して
\((k^2-4)a^2+2(5k-10)a+1>0\)・・・①
(ア)\(k^2-4=0\) つまり \(k=±2\) のとき
\(k=2\) では①が
\(1>0\) となり、任意の\(a\)について成り立つので適する。
\(k=-2\) では①が
\(-40a+1>0\) となり、任意の\(a\)については成り立たないので不適。
よって \(k=2\)
(イ)\(k^2-4<0\) のとき
①の左辺を\(a\)の2次関数とみると上に凸の放物線となり、負になる部分があるため不適。
(ウ)\(k^2-4>0\) つまり \(k<-2\) or \(k>2\) のとき
①の左辺を\(a\)の2次関数とみると下に凸の放物線だから、任意の\(a\)について①が成り立つためには
\(\displaystyle\frac{D}{4}<0\)
\((5k-10)^2-(k^2-4)<0\)
\(6k^2-25k+26>0\)
\((6k-13)(k-2)<0\)
\(2<k<\displaystyle\frac{13}{6}\)
したがって
\(2≦k<\displaystyle\frac{13}{6}\)
(2)
2点の\(x\)座標は(1)で\(y\)を消去した最初の式(i)の2解になります。
面積を求める際に必要な2解の差は、解と係数の関係でも、解の公式から具体的に2解を出してもよいです。
(1)より
\(x^2-(ka+5)x+a^2+5a+6=0\)・・・(i)
この方程式の2解を\(α,β\) (\(α<β\)) とおくと解の公式から
\(x=\displaystyle\frac{ka+5±\sqrt{D’}}{2}\) より
\(β-α=\sqrt{D’}\)

面積\(S\)は
\(S=\displaystyle\int_α^β\{kax-a^2-5a-(x^2-5x+6)\}dx\)
\(=\displaystyle\int_α^β-(x-α)(x-β)dx\)
\(=\displaystyle\frac{1}{6}(β-α)^3\)
\(=\displaystyle\frac{1}{6}(\sqrt{D’})^3\)
よって\(\sqrt{D’}\)、つまり \(D’\)が\(a\)の値によらず一定になれば面積\(S\)が一定になるので
\(D’=(ka+5)^2-4(a^2+5a+6)=(一定)\)
\(P\)を定数として
\((k^2-4)a^2+10(k-2)a+1=P\) より
\(D’\)が一定になるには
\(k^2-4=0\) かつ \(k-2=0\)
したがって
\(k=2\) ((1)で求めた範囲にある)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→奇関数・偶関数と定積分 back→面積の計算①(基礎)