接線に関する面積の問題について見ていきます。
接線と面積①②で具体的な例題を扱って、接線と面積③で総まとめをしていきます。
(例題1)
原点から放物線 \(y=x^2+ax+b^2\) に引いた2本の接線の接点を\(P,Q\)とする。このとき次の問いに答えよ。ただし \(b>0\) とする。
(1)接線の方程式、および、接点の座標を求めよ。
(2)線分\(PQ\)と放物線で囲まれた図形の面積を\(S_1\), 2本の接線と放物線で囲まれた図形の面積を\(S_2\)とするとき、\(S_1\)と\(S_2\)との比を求めよ。
(解答)
(1)
接線を \(y=mx\) とおいて重解条件を考えてもよいです。
接点の座標を \((t,t^2+at+b^2)\) とする。
\(y’=2x+a\) より、接線の方程式は
\(y=(2t+a)(x-t)+t^2+at+b^2\)
整理して
\(y=(2t+a)x-t^2+b^2\)・・・①
これが原点を通るから
\(0=-t^2+b^2\)
\(t=±b\)
したがって接線の方程式は①より
\(y=(a+2b)x\), \(y=(a-2b)x\)
接点の座標は
\((b,ab+2b^2)\), \((-b,-ab+2b^2)\)
(2)
\(S_2\)は、下側の直線(接線)が2本の接線の交点(この例題だと原点)を境目に変わるので2つの部分に分けて計算します。その際には、2次関数と接線の方程式の差が \((x-t)^2\) の形になることを利用します。
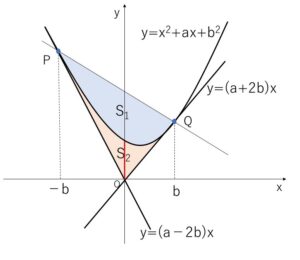
直線\(PQ\)の方程式を \(y=kx+l\) とおくと
\(S_1=\displaystyle\int_{-b}^{b}\{kx+l-(x^2+ax+b^2)\}dx\)
\(=-\displaystyle\int_{-b}^{b}(x+b)(x-b)dx\)
\(=\displaystyle\frac{1}{6}(b+b)^3\)
\(=\displaystyle\frac{4}{3}b^3\)
\(S_2\)については、\(x=0\)の前後で分けると
\(S_2\)\(=\displaystyle\int_{-b}^{0}\{x^2+ax+b^2-(a-2b)x\}dx+\displaystyle\int_{0}^{b}\{x^2+ax+b^2-(a+2b)x\}dx\)
\(=\displaystyle\int_{-b}^{0}(x+b)^2dx+\displaystyle\int_{0}^{b}(x-b)^2dx\)
\(=\left[\displaystyle\frac{(x+b)^3}{3}\right]_{-b}^{0}+\left[\displaystyle\frac{(x-b)^3}{3}\right]_{0}^{b}\)
\(=\displaystyle\frac{b^3}{3}+\displaystyle\frac{b^3}{3}\)
\(=\displaystyle\frac{2}{3}b^3\)
したがって
\(S_1:S_2=2:1\)
(例題2)
2つの放物線
\(C_1:y=x^2-5x+7\), \(C_2:y=x^2+3x-1\)
の両方に接する直線を\(l\)とする。
(1)直線\(l\)の方程式を求めよ。
(2)放物線\(C_1,C_2\)と直線\(l\)とで囲まれた図形の面積を求めよ。
(解答)
(1)
\(C_1:y=x^2-5x+7\) 上の接点を \((t,t^2-5t+7)\) とおくと、接線の方程式は
\(y’=2x-5\) より
\(y=(2t-5)(x-t)+t^2-5t+7\)
整理して
\(y=(2t-5)x-t^2+7\)・・・①
これが \(C_2:y=x^2+3x-1\) にも接するから
\((2t-5)x-t^2+7=x^2+3x-1\)
つまり
\(x^2+2(4-t)x+t^2-8=0\)・・・② が重解をもつ。
\(\displaystyle\frac{D}{4}=0\) より
\((4-t)^2-(t^2-8)=0\)
\(t=3\)
①より接線の方程式は
\(y=x-2\)
(2)
積分計算に必要な情報は、「\(C_1,C_2\)における接点の\(x\)座標」と「放物線\(C_1,C_2\)どうしの交点の\(x\)座標」です。
放物線と接線の差をとると\((x-t)^2\)の形になることに着目すると計算が楽になります。
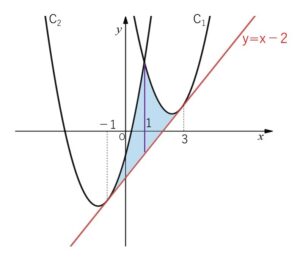
\(C_1\)における接点の\(x\)座標は(1)より
\(x=t=3\)
\(C_2\)における接点の\(x\)座標は(1)②式より
\(x^2+2x+1=0\)
\((x+1)^2=0\)
\(x=-1\)
\(C_1:y=x^2-5x+7\), \(C_2:y=x^2+3x-1\)
の交点の\(x\)座標は
\(x^2-5x+7=x^2+3x-1\) より
\(x=1\)
したがって面積\(S\)は
\(S=\displaystyle\int_{-1}^{1}\{x^2+3x-1-(x-2)\}dx+\displaystyle\int_{1}^{3}\{x^2-5x+7-(x-2)\}dx\)
\(=\displaystyle\int_{-1}^{1}(x+1)^2dx+\displaystyle\int_{1}^{3}(x-3)^2dx\)
\(=\left[\displaystyle\frac{(x+1)^3}{3}\right]_{-1}^{1}+\left[\displaystyle\frac{(x-3)^3}{3}\right]_{1}^{3}\)
\(=\displaystyle\frac{8}{3}+\displaystyle\frac{8}{3}\)
\(=\displaystyle\frac{16}{3}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接線と面積② back→面積比・面積の等分