対称性に関する定積分について見ていきます。
・対称性と定積分(King Property)
連続関数\(f(x)\)について、次の等式が成り立ちます。(King property と呼ばれる)
\(\displaystyle\int_{a}^{b}f(x)dx=\displaystyle\int_{a}^{b}f(a+b-x)dx\)
(解説)
証明は次のように置換積分を利用して簡単にできます。
(証明)
\(x=a+b-t\) の置換をすると
\(\displaystyle\int_{a}^{b}f(x)dx\)
\(=\displaystyle\int_{b}^{a}f(a+b-t)(-dt)\)
\(=\displaystyle\int_{a}^{b}f(a+b-t)dt\)
\(=\displaystyle\int_{a}^{b}f(a+b-x)dx\) (定積分では積分変数は何でもよい)
また、\(y=f(x)\) と \(y=f(a+b-x)\) のグラフが 直線 \(x=\displaystyle\frac{a+b}{2}\) について線対称であることから(下注参照)、この等式が成り立つことが図形的も分かります。
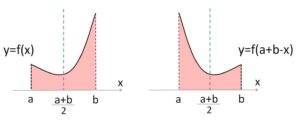
King Property のよいところは、原始関数を求めるのが困難な場合、\(f(a+b-x)\) の定積分が同じ値になることから、\(f(x)\) と \(f(a+b-x)\) を定数倍・足し引きなどをして組み合わせた場合に、できた関数の原始関数を求めることができる場合、もとの定積分の値が分かるというところにあります。つまり
\(I=\displaystyle\int_{a}^{b}f(x)dx=\displaystyle\int_{a}^{b}f(a+b-x)dx\)
なので、例えば \(f(x)+f(a+b-x)=\sin x\) になる場合
\(2I=\displaystyle\int_{a}^{b}\{f(x)+f(a+b-x)\}dx=\displaystyle\int_{a}^{b}\sin xdx\)
より、定積分\(I\)の値が分かるということです。
なお実際に問題で活用する場合には、King Property の等式をそのまま利用するよりは、証明のように置換積分を利用した方がよいと思います。問題では上端と下端が、\(\displaystyle\int_{0}^{a}\) か \(\displaystyle\int_{-a}^{a}\) の形の場合が大半なので、この手の積分では
\(x=a-t\) か \(x=-t\)
の置換をする場合がほとんどです。また関数\(f(x)\)については、三角関数や指数関数が扱われることが多いです。
(注)\(x=k\) について対称なグラフ
\(y=f(x)\) を 直線 \(x=k\) について対称移動したグラフの方程式は
\(y=f(2k-x)\) となる。
(証明)
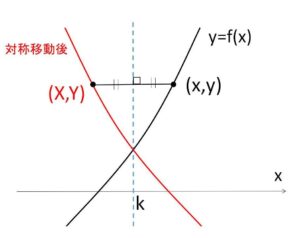
\(y=f(x)\) 上の点 \((x,y)\) を対称移動した点を \((X,Y)\) とする。
\(\displaystyle\frac{x+X}{2}=k\)、\(y=Y\)
だから
\(x=2k-X\)・・・①
\(y=Y\)・・・②
\(y=f(x)\) に①②を代入すると
\(Y=f(2k-X)\)
あとは、変数を\(x,y\)にすればよい。
したがって、\(y=f(a+b-x)\) のグラフは \(y=f(x)\) のグラフを \(x=\displaystyle\frac{a+b}{2}\) について対称移動したものになる。
(例題)
(1)\(\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\sin x}{\sin x+\cos x}dx\) を求めよ。
(2)\(\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\cos^3x}{\sin x+\cos x}dx\) を求めよ。
(1)に関しては別解もあるので、そちらもやっておきます。
(解答)
(1)
\(I=\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\sin x}{\sin x+\cos x}dx\)
\(x=\displaystyle\frac{π}{2}-t\) の置換をすると
\(I=\displaystyle\int_{\frac{π}{2}}^{0}\displaystyle\frac{\sin (\displaystyle\frac{π}{2}-t)}{\sin (\displaystyle\frac{π}{2}-t)+\cos (\displaystyle\frac{π}{2}-t)}(-dt)\)
\(I=\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\cos t}{\cos t+\sin t}dt\)
よって
\(I+I=\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\sin x}{\sin x+\cos x}dx+\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\cos x}{\sin x+\cos x}dx\)
となるから
\(2I=\displaystyle\int_{0}^{\frac{π}{2}}dx\)
\(I=\displaystyle\frac{π}{4}\)
(別解)
\(I=\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\sin x}{\sin x+\cos x}dx\)・・・①
\(J=\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\cos x}{\sin x+\cos x}dx\)・・・②
とおく。①+② より
\(I+J=\displaystyle\int_{0}^{\frac{π}{2}}dx\)
よって
\(I+J=\displaystyle\frac{π}{2}\)・・・③
②-① より
\(-I+J=\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\cos x-\sin x}{\sin x+\cos x}dx\)
よって
\(-I+J=\left[\log|\sin x+\cos x|\right]_{0}^{\frac{π}{2}}\)
\(-I+J=0\)・・・④
(③-④)÷2 より
\(I=\displaystyle\frac{π}{4}\)
(\(J\)も同じ値になる)
\(=\displaystyle\frac{1}{2}\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{(\sin x+\cos x)+(\sin x-\cos x)}{\sin x+\cos x}dx\)
\(=\displaystyle\frac{1}{2}\displaystyle\int_{0}^{\frac{π}{2}}(1-\displaystyle\frac{\cos x-\sin x}{\sin x+\cos x})dx\)
として解いてもよいです。やってることは別解とほとんど同じです。
これらの方法をとると不定積分も求めることができます。
(2)
\(K=\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\cos^3x}{\sin x+\cos x}dx\)
\(x=\displaystyle\frac{π}{2}-t\) で置換すると
\(K=\displaystyle\int_{\frac{π}{2}}^{0}\displaystyle\frac{\cos^3(\displaystyle\frac{π}{2}-t)}{\sin (\displaystyle\frac{π}{2}-t)+\cos (\displaystyle\frac{π}{2}-t)}(-dt)\)
\(K=\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\sin^3t}{\cos t+\sin t}dt\)
よって
\(K+K=\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{\sin^3x+\cos^3x}{\sin x+\cos x}dx\)
\(2K=\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{(\sin x+\cos x)(\sin^2x-\sin x\cos x+\cos^2x)}{\sin x+\cos x}dx\)
\(2K=\displaystyle\int_{0}^{\frac{π}{2}}(1-\displaystyle\frac{1}{2}\sin2x)dx\)
\(2K=\left[x+\displaystyle\frac{1}{4}\cos2x\right]_{0}^{\frac{π}{2}}\)
\(2K=\displaystyle\frac{π}{2}+\displaystyle\frac{1}{4}(-1-1)\)
したがって
\(K=\displaystyle\frac{π-1}{4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→対称性と定積分② back→定積分と漸化式③(β関数)