定積分と無限級数の例題です。
①長方形の短冊等の面積との比較
②関数の大小より定積分の大小を導く
です。
(例題1)
次の無限級数の収束・発散を調べよ。(収束する場合には極限値は求めなくてよい)
(1)\(1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4}+\cdots\)
(2)\(1+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\displaystyle\frac{1}{\sqrt{4}}+\cdots\)
(3)\(1+\displaystyle\frac{1}{2^2}+\displaystyle\frac{1}{3^2}+\displaystyle\frac{1}{4^2}+\cdots\)
(解答)
先に答えだけ書くと
(1)発散 (2)発散 (3)収束
(1)
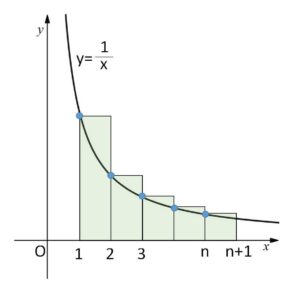
図より
\(1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\cdots+\displaystyle\frac{1}{n}>\displaystyle\int_{1}^{n+1}\displaystyle\frac{1}{x}dx\)
\(\displaystyle\int_{1}^{n+1}\displaystyle\frac{1}{x}dx=\log(n+1)\) だから
\(1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\cdots+\displaystyle\frac{1}{n}>\log(n+1)\)
よって \(\displaystyle\lim_{n \to \infty}\log(n+1)=\infty\) だから
無限級数 \(1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4}+\cdots\) は発散する。
(2)
\(1+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}>1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\cdots+\displaystyle\frac{1}{n}\)
より発散がすぐに分かりますが、せっかくなので(2)も定積分で比較してみます。
(1)と同様に
\(1+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}>\displaystyle\int_{1}^{n+1}\displaystyle\frac{1}{\sqrt{x}}dx\)
\(\displaystyle\int_{1}^{n+1}\displaystyle\frac{1}{\sqrt{x}}dx=2\sqrt{n+1}-2\) だから
\(1+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}>2\sqrt{n+1}-2\)
よって \(\displaystyle\lim_{n \to \infty}(2\sqrt{n+1}-2)=\infty\) だから
無限級数 \(1+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\displaystyle\frac{1}{\sqrt{4}}+\cdots\) は発散する。
(3)
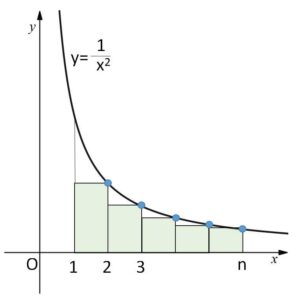
図より
\(\displaystyle\frac{1}{2^2}+\displaystyle\frac{1}{3^2}+\cdots+\displaystyle\frac{1}{n^2}<\displaystyle\int_{1}^{n}\displaystyle\frac{1}{x^2}dx\)
両辺に\(1\)を加えると
\(1+\displaystyle\frac{1}{2^2}+\displaystyle\frac{1}{3^2}+\cdots+\displaystyle\frac{1}{n^2}<1+\displaystyle\int_{1}^{n}\displaystyle\frac{1}{x^2}dx\)
\(\displaystyle\int_{1}^{n}\displaystyle\frac{1}{x^2}dx=-\displaystyle\frac{1}{n}+1\) だから
\(1+\displaystyle\frac{1}{2^2}+\displaystyle\frac{1}{3^2}+\cdots+\displaystyle\frac{1}{n^2}<2-\displaystyle\frac{1}{n}\)
\(\displaystyle\lim_{n \to \infty}(2-\displaystyle\frac{1}{n})=0\) より
無限級数 \(1+\displaystyle\frac{1}{2^2}+\displaystyle\frac{1}{3^2}+\displaystyle\frac{1}{4^2}+\cdots\) は収束する。・・・(注)
(注)
厳密には数列
\(a_n=1+\displaystyle\frac{1}{2^2}+\displaystyle\frac{1}{3^2}+\cdots+\displaystyle\frac{1}{n^2}\)
が、上に有界な単調増加数列であることから収束することが言える(高校数学範囲外の定理)。上に有界とは簡単にいうと天井がある(ある値より常に小さい)ということで、(3)よりそれは\(2\)より小さいというである。単調増加数列であることは長方形の面積が増えていくことから分かる。
もし上に有界な単調増加数列でない場合、収束することが言えないことがある。
例えば \(\cos n<1+\displaystyle\frac{1}{n}\) であるが、\(\cos n\) は振動し収束しない。(上に有界ではあるが、単調増加数列でないから収束すると結論づけれない)
なおこの\(a_n\)は\(\displaystyle\frac{π^2}{6}\)に収束します。(バーゼル問題)
結果だけでも知っておくとよいでしょう。
※本問を一般化すると
無限級数
\(1+\displaystyle\frac{1}{2^{p}}+\displaystyle\frac{1}{3^{p}}+\displaystyle\frac{1}{4^{p}}+\cdots \)
は \(p≦1\) のとき発散し、\(p>1\) のとき収束することになる。これは積分結果で\(n\)のどういう式で表されるかに由来します。例えば本問だと \(p=1,\displaystyle\frac{1}{2}\) のときは、それぞれ \(\log(n+1),\sqrt{n+1}\) が現れるので発散し、\(p=2\) のとき \(\displaystyle\frac{1}{n}\) が現れるので収束といった具合になります。
(例題2)
数列\(\{a_n\}_{n=1,2,3,\cdots}\) を
\(a_n=\displaystyle\frac{1}{n!}\displaystyle\int_{0}^{1}t^{n}e^{-t}dt\)
で定める。ここで\(e\)は自然対数の底とする。次の問いに答えよ。
(1)\(0≦\displaystyle\int_{0}^{1}t^{n}e^{-t}dt≦1-e^{-1}\) (\(n=1,2,3,\cdots\)) を示せ。
(2)\(\displaystyle\lim_{n \to \infty}a_n=0\) を示せ。
(3)\(a_{n+1}=a_n-\displaystyle\frac{1}{(n+1)!e}\) (\(n=1,2,3,\cdots\)) を示せ。
(4)\(e=1+\displaystyle\sum_{n=1}^{\infty}\displaystyle\frac{1}{n!}\) を示せ。
(解答)
(1)
なお(1)は(2)のための誘導ですが、\(a_n \to 0\) は \(t^n\) の方を残しても示すことができます。
\(a_n=\displaystyle\frac{1}{n!}\displaystyle\int_{0}^{1}t^{n}e^{-t}dt\)
\(0≦t≦1\) のとき
\(0≦t^{n}≦1\) だから
\(0≦t^{n}e^{-t}≦e^{-t}\) (\(e^{-t}>0\) より)
よって
\(0≦\displaystyle\int_{0}^{1}t^{n}e^{-t}dt≦\displaystyle\int_{0}^{1}e^{-t}dt\)
となるから
\(0≦\displaystyle\int_{0}^{1}t^{n}e^{-t}dt≦-e^{-1}+1\)
(2)
(1)の不等式の辺々を\(n!\)で割ると
\(0≦a_n≦\displaystyle\frac{-e^{-1}+1}{n!}\)
よってはさみうちの原理より
\(\displaystyle\lim_{n \to \infty}a_n=0\)
(3)
\(a_{n+1}=\displaystyle\frac{1}{(n+1)!}\displaystyle\int_{0}^{1}t^{n+1}e^{-t}dt\)
\(=\displaystyle\frac{1}{(n+1)!}\left[t^{n+1}(-e^{-t})\right]_{0}^{1}-\displaystyle\frac{1}{(n+1)!}\displaystyle\int_{0}^{1}(n+1)t^{n}(-e^{-t})dt\)
\(=-\displaystyle\frac{e^{-1}}{(n+1)!}+\displaystyle\frac{1}{n!}\displaystyle\int_{0}^{1}t^{n}e^{-t}dt\)
よって
\(a_{n+1}=a_n-\displaystyle\frac{1}{(n+1)!e}\)
(4)
階差型の漸化式は、\(n≧2\) と \(n=1\) で場合分けが必要ですが、最終的に \(n \to \infty\) を考えるので、今回は \(n≧2\) だけでよいです。
\(a_{n+1}=a_n-\displaystyle\frac{1}{(n+1)!e}\) より
\(n≧2\) のとき
\(a_n=a_1-\displaystyle\sum_{k=1}^{n-1}\displaystyle\frac{1}{(k+1)!e}\)
ここで
\(a_1=\displaystyle\frac{1}{1!}\displaystyle\int_{0}^{1}te^{-t}dt\)
(部分積分をする)
\(=[t(-e^{-t})]_{0}^{1}+\displaystyle\int_{0}^{1}e^{-t}dt\)
\(=-e^{-1}+(-e^{-1}+1)\)
\(=1-\displaystyle\frac{2}{e}\) だから
\(a_n=1-\displaystyle\frac{2}{e}-\displaystyle\frac{1}{e}\displaystyle\sum_{k=1}^{n-1}\displaystyle\frac{1}{(k+1)!}\)
\(a_n=1-\displaystyle\frac{2}{e}-\displaystyle\frac{1}{e}\left(\displaystyle\frac{1}{2!}+\displaystyle\frac{1}{3!}+\cdots+\displaystyle\frac{1}{n!}\right)\)
\(=1-\displaystyle\frac{1}{e}\left(1+1+\displaystyle\frac{1}{2!}+\displaystyle\frac{1}{3!}+\cdots+\displaystyle\frac{1}{n!}\right)\)
\(=1-\displaystyle\frac{1}{e}\left(1+\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{k!}\right)\)
よって
\(e(1-a_n)=1+\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{k!}\)
\(n \to \infty\) とすると、(2)の結果 \(a_n \to 0\) より
\(e=1+\displaystyle\sum_{k=1}^{\infty}\displaystyle\frac{1}{k!}\)
したがって変数を変えると
\(e=1+\displaystyle\sum_{n=1}^{\infty}\displaystyle\frac{1}{n!}\)
(参考)
\(0!=1\) なので、(4)の結果から
\(e=\displaystyle\sum_{n=0}^{\infty}\displaystyle\frac{1}{n!}=\displaystyle\frac{1}{0!}+\displaystyle\frac{1}{1!}+\displaystyle\frac{1}{2!}+\displaystyle\frac{1}{3!}+\cdots\)
(\(e\)の無限級数による表示)
となります。これはマクローリン展開(高校範囲外)に関係しています。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→定積分と無限級数②(メルカトル級数・ライプニッツ級数) back→漸化式と定積分と極限