メルカトル級数とライプニッツ級数について見ていきます。
・メルカトル級数・ライプニッツ級数
次の2つの無限級数はそれぞれ \(\log 2, \ \displaystyle\frac{π}{4}\) に収束します。
(メルカトル級数)
\(\displaystyle\sum_{k=1}^{\infty}\displaystyle\frac{(-1)^{k-1}}{k}=1-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}+\cdots=\log 2\)
(自然数の逆数の交代級数(符号が交互に入れ替わる)は収束)
(ライプニッツ級数)
\(\displaystyle\sum_{k=1}^{\infty}\displaystyle\frac{(-1)^{k-1}}{2k-1}=1-\displaystyle\frac{1}{3}+\displaystyle\frac{1}{5}-\displaystyle\frac{1}{7}+\cdots=\displaystyle\frac{π}{4}\)
(奇数の逆数の交代級数は収束)
これらの証明は例題で扱いたいと思います。主に次の2つの方法があります。
(i)等比数列型の\(x\)の整式を用いる方法
(ii)\(\tan^nx\) (\(\tan^{2n}x\)) の定積分を利用する方法
(i)では等比数列の和
\(1-x+x^2-x^3+\cdots+(-1)^{n-1}x^{n-1}=\displaystyle\frac{1-(-x)^{n}}{1+x}\)
がポイントになります。左辺から右辺に変形するのは分かりやすいと思いますが、たまに右辺から左辺の変形をする場合もあるので両方おさえておきましょう。
また、積分とシグマの計算をすることもあるので、どちらかに統一する必要がでてくることがあります。
(例題1)
(1)自然数\(n\)に対して
\(R_n(x)=\displaystyle\frac{1}{1+x}-\{1-x+x^2-\cdots+(-1)^{n}x^n\}\)
とするとき
\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{1}R_n(x)dx\)、\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{1}R_n(x^2)dx\) をそれぞれ求めよ。
(2) (1)を利用して、次の無限級数の和を求めよ。
(ア)\(1-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}+\cdots\)
(イ)\(1-\displaystyle\frac{1}{3}+\displaystyle\frac{1}{5}-\displaystyle\frac{1}{7}+\cdots\)
\(\displaystyle\int_{0}^{1}R_n(x)dx=\displaystyle\int_{0}^{1}\displaystyle\frac{1}{1+x}dx-\displaystyle\int_{0}^{1}(1-x+x^2+\cdots)dx\)
となるので、\(\log 2\) や \(1-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\cdots\) などが見えてきますが、(1)ではまず等比数列の和を使って\(R_{n}(x)\) を簡単な式にします。
一応細かいことを言っておくと、\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{1}R_n(x)dx\) は積分してから\(n \to \infty\)をするという意味です。この順番は逆にしてはいけません。
(解答)
(1)
\(x≠-1\) のとき
\(R_n(x)=\displaystyle\frac{1}{1+x}-\{1-x+x^2-\cdots+(-1)^{n}x^n\}\)
\(=\displaystyle\frac{1}{1+x}-\displaystyle\frac{1-(-x)^{n+1}}{1-(-x)}\)
\(=\displaystyle\frac{(-x)^{n+1}}{1+x}\)
となりますが、この式のままでは計算できないので、不等式ではさみこむことになります。文字\(n\)を残すようにするのがポイントですが、\((-x)\) の \(-\) が邪魔なのでこれは分離しておきます。
ここで、メルカトル級数のことを知っていればこの積分が\(0\)に収束することが予測できますが(\(\displaystyle\int_{0}^{1}\displaystyle\frac{1}{1+x}dx=\log 2\) より分かる)、もし知らない場合にはかなり大雑把になってしまいますが、\(x^n\) は\(n\)が十分大きいときには \(0≦x<1\) ではほぼ\(0\)で、\(x=1\) のときだけ \(x^n=1\) となるので、面積はほとんど\(0\)という予測をたてることになります。
よって
\(\displaystyle\int_{0}^{1}R_n(x)dx=(-1)^{n+1}\displaystyle\int_{0}^{1}\displaystyle\frac{x^{n+1}}{1+x}dx\)
ここで、\(0≦x≦1\) のとき
\(\displaystyle\frac{1}{2}≦\displaystyle\frac{1}{1+x}≦1\) だから
\(\displaystyle\frac{1}{2}x^{n+1}≦\displaystyle\frac{x^{n+1}}{1+x}≦x^{n+1}\)
ゆえに
\(\displaystyle\int_{0}^{1}\displaystyle\frac{1}{2}x^{n+1}dx≦\displaystyle\int_{0}^{1}\displaystyle\frac{x^{n+1}}{1+x}dx≦\displaystyle\int_{0}^{1}x^{n+1}dx\)
\(\displaystyle\frac{1}{2(n+2)}≦\displaystyle\int_{0}^{1}\displaystyle\frac{x^{n+1}}{1+x}dx≦\displaystyle\frac{1}{n+2}\)
はさみうちの原理から
\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{1}\displaystyle\frac{x^{n+1}}{1+x}dx=0\)
したがって
\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{1}R_n(x)dx=0\)
(丁寧にやるなら絶対値をとって \(\left|\displaystyle\int_{0}^{1}R_n(x)dx\right|=\left|\displaystyle\int_{0}^{1}\displaystyle\frac{x^{n+1}}{1+x}dx\right|\to 0\) とすればよい)
同様に\(R_{n}(x^2)\) については、\(x \to x^2\) とすれば
\(\displaystyle\int_{0}^{1}R_n(x^2)dx=(-1)^{n+1}\displaystyle\int_{0}^{1}\displaystyle\frac{x^{2n+2}}{1+x^2}dx\) であり
\(0≦x≦1\) のとき
\(\displaystyle\frac{1}{2}x^{2n+2}≦\displaystyle\frac{x^{2n+2}}{1+x^2}≦x^{2n+2}\)
ゆえに
\(\displaystyle\int_{0}^{1}\displaystyle\frac{1}{2}x^{2n+2}dx≦\displaystyle\int_{0}^{1}\displaystyle\frac{x^{2n+2}}{1+x^2}dx≦\displaystyle\int_{0}^{1}x^{2n+2}dx\)
\(\displaystyle\frac{1}{2(2n+3)}≦\displaystyle\int_{0}^{1}\displaystyle\frac{x^{2n+2}}{1+x^2}dx≦\displaystyle\frac{1}{2n+3}\)
はさみうちの原理から
\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{1}\displaystyle\frac{x^{2n+2}}{1+x^2}dx=0\)
したがって
\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{1}R_n(x^2)dx=0\)
(2)
\(\displaystyle\int_{0}^{1}R_n(x)dx=\displaystyle\int_{0}^{1}\displaystyle\frac{1}{1+x}dx-\displaystyle\int_{0}^{1}\{1-x+x^2-\cdots+(-1)^{n}x^n\}dx\)
\(=[\log|1+x|]_{0}^{1}-\left[x-\displaystyle\frac{x^2}{2}+\displaystyle\frac{x^3}{3}-\cdots+\displaystyle\frac{(-1)^{n}x^{n+1}}{n+1}\right]_{0}^{1}\)
\(=\log2-\left(1-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}-\cdots+\displaystyle\frac{(-1)^{n}}{n+1}\right)\)
よって \(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{1}R_n(x)dx=0\) より
\(1-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}+\cdots=\log2\)
同様に
\(\displaystyle\int_{0}^{1}R_n(x^2)dx=\displaystyle\int_{0}^{1}\displaystyle\frac{1}{1+x^2}dx-\displaystyle\int_{0}^{1}\{1-x^2+x^4-\cdots+(-1)^{n}x^{2n}\}dx\)
(1つ目は \(x=\tanθ\) の置換をして)
\(=\displaystyle\int_{0}^{\frac{π}{4}}dθ-\left[x-\displaystyle\frac{x^3}{3}+\displaystyle\frac{x^5}{5}-\cdots+\displaystyle\frac{(-1)^{n}x^{2n+1}}{2n+1}\right]_{0}^{1}\)
\(=\displaystyle\frac{π}{4}-\left(1-\displaystyle\frac{1}{3}+\displaystyle\frac{1}{5}-\cdots+\displaystyle\frac{(-1)^{n}}{2n+1}\right)\)
\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{1}R_n(x^2)dx=0\) より
\(1-\displaystyle\frac{1}{3}+\displaystyle\frac{1}{5}-\displaystyle\frac{1}{7}+\cdots=\displaystyle\frac{π}{4}\)
(例題2)
自然数\(n\)に対して
\(a_n=\displaystyle\int_{0}^{\frac{π}{4}}(\tan x)^{2n}dx\)
とおく。このとき、以下の問いに答えよ。
(1)\(a_1\)を求めよ。
(2)\(a_{n+1}\)を\(a_n\)で表せ。
(3)\(\displaystyle\lim_{n \to \infty}a_n\)を求めよ。
(4)\(\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{(-1)^{k+1}}{2k-1}\) を求めよ。
(解答)
(1)
\(a_1=\displaystyle\int_{0}^{\frac{π}{4}}\tan^2xdx\)
\(=\displaystyle\int_{0}^{\frac{π}{4}}(\displaystyle\frac{1}{\cos^2x}-1)dx\)
\(=[\tan x-x]_{0}^{\frac{π}{4}}\)
\(=1-\displaystyle\frac{π}{4}\)
(2)
(\(\tan\)の漸化式は、\(\tan^2x\) をつまみ出すのが基本です)
\(a_{n+1}=\displaystyle\int_{0}^{\frac{π}{4}}(\tan x)^{2(n+1)}dx\)
\(=\displaystyle\int_{0}^{\frac{π}{4}}(\tan x)^{2n}\tan^2x dx\)
\(=\displaystyle\int_{0}^{\frac{π}{4}}(\tan x)^{2n}(\displaystyle\frac{1}{\cos^2x}-1)dx\)
\(=\displaystyle\int_{0}^{\frac{π}{4}}(\tan x)^{2n}\cdot\displaystyle\frac{1}{\cos^2x}dx-\displaystyle\int_{0}^{\frac{π}{4}}(\tan x)^{2n}dx\)
(1つ目は導関数接触型で積分計算可能です)
\(=\left[\displaystyle\frac{(\tan x)^{2n+1}}{2n+1}\right]_{0}^{\frac{π}{4}}-a_n\)
\(=\displaystyle\frac{1}{2n+1}-a_n\)
(3)
極限の大雑把な予想ですが、\(\tan x\) は \(0≦x<\displaystyle\frac{π}{4}\) のとき \(0≦\tan x<1\) なので、\(\tan^{2n} x\) は\(n\)が十分大きいとき区間でほぼ\(0\)なので、\(0\)に収束することが予想できます。
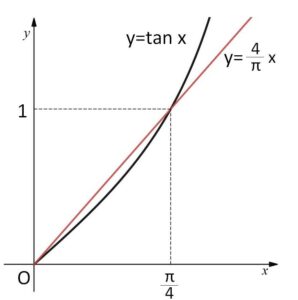
\(y=\tan x\) について
\(y’=\displaystyle\frac{1}{\cos^2x}\)、\(y”=\displaystyle\frac{2\sin x}{\cos^3x}\)
より、\(0<x≦\displaystyle\frac{π}{4}\) で下に凸。
よって図の直線は上側にあるので
\(0≦\tan x≦\displaystyle\frac{4}{π}x\)
ゆえに
\(0≦\displaystyle\int_{0}^{\frac{π}{4}}(\tan x)^{2n}dx≦\displaystyle\int_{0}^{\frac{π}{4}}(\displaystyle\frac{4}{π}x)^{2n}dx\)
\(0≦a_n≦(\displaystyle\frac{4}{π})^{2n}\left[\displaystyle\frac{x^{2n+1}}{2n+1}\right]_{0}^{\frac{π}{4}}\)
\(0≦a_n≦\displaystyle\frac{π}{4}\cdot\displaystyle\frac{1}{2n+1}\)
したがってはさみうちの原理より
\(\displaystyle\lim_{n \to \infty}a_n=0\)
(別解)漸化式を利用
\(a_n\) (\(a_{n+1}\)) は面積を考えると正の値。
(2)より
\(a_n=\displaystyle\frac{1}{2n+1}-a_{n+1}<\displaystyle\frac{1}{2n+1}\)
よって
\(0<a_n<\displaystyle\frac{1}{2n+1}\)
したがってはさみうちの原理より
\(\displaystyle\lim_{n \to \infty}a_n=0\)
(4)
漸化式は両辺で1つ違いにするのが基本なので、\((-1)^{n+1}\) を掛けます。
(2)より (\(n\)を1つ下げて)
\(a_{n}=-a_{n-1}+\displaystyle\frac{1}{2n-1}\)
\((-1)^{n+1}\) を両辺に掛けると
\((-1)^{n+1}a_{n}=(-1)^{n}a_{n-1}+\displaystyle\frac{(-1)^{n+1}}{2n-1}\) (階差型)
\((-1)^{n+1}a_n=b_n\)とおくと
\(b_1=(-1)^2a_1=1-\displaystyle\frac{π}{4}\)
\(b_n=b_{n-1}+\displaystyle\frac{(-1)^{n+1}}{2n-1}\)
\(n≧2\) のとき
\(b_n=b_1+\displaystyle\sum_{k=2}^{n}\displaystyle\frac{(-1)^{k+1}}{2k-1}\) (階差には\(n=2,3,\cdots\) と代入していくので、\(k=2\) スタートになる)
よって
\(b_n=1-\displaystyle\frac{π}{4}+\displaystyle\sum_{k=2}^{n}\displaystyle\frac{(-1)^{k+1}}{2k-1}\)
(\(1\)をシグマに組み込んで)
\(b_n=\displaystyle\sum_{k=1}^{n}\displaystyle\frac{(-1)^{k+1}}{2k-1}-\displaystyle\frac{π}{4}\)
したがって
\((-1)^{n+1}a_n=\displaystyle\sum_{k=1}^{n}\displaystyle\frac{(-1)^{k+1}}{2k-1}-\displaystyle\frac{π}{4}\)
\(\displaystyle\lim_{n \to \infty}a_n=0\) より \(n \to \infty\) のとき (左辺)\(\to 0\) だから
\(\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{(-1)^{k+1}}{2k-1}=\displaystyle\frac{π}{4}\)
(例題3)
\(n\)を\(2\)以上の自然数とする。
(1)\(0≦x≦1\) のとき、次の不等式が成り立つことを示せ。
\(\displaystyle\frac{1}{2}x^n≦(-1)^{n}\left\{\displaystyle\frac{1}{x+1}-1-\displaystyle\sum_{k=2}^{n}(-x)^{k-1}\right\}≦x^n-\displaystyle\frac{1}{2}x^{n+1}\)
(2)
\(a_n=\displaystyle\sum_{k=1}^{n}\displaystyle\frac{(-1)^{k-1}}{k}\) とするとき、次の極限値を求めよ。
\(\displaystyle\lim_{n \to \infty}(-1)^{n}n(a_n-\log 2)\)
(解答)
(1)
(まずは、シグマの部分を等比数列の和を用いて簡単にします)
(中辺)\(=(-1)^{n}\left\{\displaystyle\frac{1}{x+1}-1-\displaystyle\sum_{k=2}^{n}(-x)^{k-1}\right\}\)
\(=(-1)^{n}\left\{\displaystyle\frac{1}{x+1}-1-\displaystyle\frac{(-x)\{1-(-x)^{n-1}\}}{1-(-x)}\right\}\)
\(=(-1)^n\displaystyle\frac{(-x)^{n}}{1+x}\)
\(=(-1)^{2n}\displaystyle\frac{x^{n}}{1+x}\)
\(=\displaystyle\frac{x^n}{1+x}\)
よって
\(\displaystyle\frac{1}{2}x^n≦\displaystyle\frac{x^n}{1+x}≦x^n-\displaystyle\frac{1}{2}x^{n+1}\)
を示せばよい。
\(0≦x≦1\) だから
(左側)
\(\displaystyle\frac{x^n}{1+x}-\displaystyle\frac{1}{2}x^n=\displaystyle\frac{2x^n-x^n(1+x)}{2(1+x)}=\displaystyle\frac{x^n(1-x)}{2(1+x)}≧0\)
(右側)
\(x^n-\displaystyle\frac{1}{2}x^{n+1}-\displaystyle\frac{x^n}{1+x}=\displaystyle\frac{(2x^n-x^{n+1})(1+x)-2x^n}{2(1+x)}\)
\(=\displaystyle\frac{x^{n+1}-x^{n+2}}{2(1+x)}=\displaystyle\frac{x^{n+1}(1-x)}{2(1+x)}≧0\)
したがって与不等式は成り立つ。
(2)
\(a_n=\displaystyle\sum_{k=1}^{n}\displaystyle\frac{(-1)^{k-1}}{k}\) (極限はメルカトル級数) を(1)からどうやって作るかを考えると、積分をすればよいことが分かります。シグマの部分の積分は分かりにくかったら項を列挙して考えるとよいです。(結局先に項別に積分してから和をとっても同じことになる)
\(\displaystyle\frac{1}{2}x^n≦(-1)^{n}\left\{\displaystyle\frac{1}{x+1}-1-\displaystyle\sum_{k=2}^{n}(-x)^{k-1}\right\}≦x^n-\displaystyle\frac{1}{2}x^{n+1}\)
において、\(x=0\) から \(x=1\) まで積分すると
\(\displaystyle\int_{0}^{1}\displaystyle\frac{1}{2}x^ndx≦(-1)^{n}\left\{\displaystyle\int_{0}^{1}\left(\displaystyle\frac{1}{x+1}-1\right)dx-\displaystyle\int_{0}^{1}\displaystyle\sum_{k=2}^{n}(-x)^{k-1}dx\right\}\)
\(\ ≦\displaystyle\int_{0}^{1}\left(x^n-\displaystyle\frac{1}{2}x^{n+1}\right)dx\)
ここで
\(\displaystyle\int_{0}^{1}\displaystyle\sum_{k=2}^{n}(-x)^{k-1}dx\)
\(=\displaystyle\int_{0}^{1}\{-x+x^2-x^3+\cdots+(-x)^{n-1}\}dx\)
\(=\left[-\displaystyle\frac{x^2}{2}+\displaystyle\frac{x^3}{3}-\displaystyle\frac{x^4}{4}+\cdots-\displaystyle\frac{(-x)^n}{n}\right]_{0}^{1}\)
\(=-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}+\cdots-\displaystyle\frac{(-1)^n}{n}\)
(これは結局 \(\displaystyle\sum_{k=2}^{n}\displaystyle\int_{0}^{1}(-x)^{k-1}dx\) と同じ。有限の範囲では順序交換OK)
\(=\displaystyle\sum_{k=2}^{n}-\displaystyle\frac{(-1)^k}{k}\)
\(=\displaystyle\sum_{k=2}^{n}\displaystyle\frac{(-1)^{k-1}}{k}\)
よって不等式は
\(\displaystyle\frac{1}{2(n+1)}≦(-1)^{n}\left\{\log2-1-\displaystyle\sum_{k=2}^{n}\displaystyle\frac{(-1)^{k-1}}{k}\right\}≦\displaystyle\frac{1}{n+1}-\displaystyle\frac{1}{2(n+2)}\)
(\(-1\)をシグマに組み込んで)
\(\displaystyle\frac{1}{2(n+1)}≦(-1)^{n}\left\{\log2-\displaystyle\sum_{k=1}^{n}\displaystyle\frac{(-1)^{k-1}}{k}\right\}≦\displaystyle\frac{1}{n+1}-\displaystyle\frac{1}{2(n+2)}\)
(\(-n\)倍して)
\(-\displaystyle\frac{n}{n+1}+\displaystyle\frac{n}{2(n+2)}≦(-1)^{n}n(a_n-\log2)≦-\displaystyle\frac{n}{2(n+1)}\)
\(-\displaystyle\frac{1}{1+\displaystyle\frac{1}{n}}+\displaystyle\frac{1}{2(1+\displaystyle\frac{2}{n})}≦(-1)^{n}n(a_n-\log2)≦-\displaystyle\frac{1}{2(1+\displaystyle\frac{1}{n})}\)
したがってはさみうちの原理より
\(\displaystyle\lim_{n \to \infty}(-1)^{n}n(a_n-\log2)=-\displaystyle\frac{1}{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→e,π が無理数であることの証明 back→定積分と無限級数①