逆関数の定積分について見ていきます。
\(y=f(x)\) と \(x=f^{-1}(y)\)
は全く同じ式(同値)であり、2式の\(x,y\)も同じです。
(例題1)
\(-1≦x≦1\) なる\(x\)に対して、\(\sin y=x\) を満たす \(-\displaystyle\frac{π}{2}≦y≦\displaystyle\frac{π}{2}\) なる区間の\(y\)を対応させる関数を \(y=f(x)\) とするとき、\(\displaystyle\int_{0}^{\frac{\sqrt{3}}{2}}f(x)dx\) の値を求めよ。
3つの解法を紹介しますが、特に1つ目と2つ目が使える範囲が広いので重要です。
なお一応断っておくと、問題文の \(\sin y=x\) と \(y=f(x)\) は同じ式で、\(x,y\)としても同じです。
(解法1)置換積分を利用
\(f'(x)dx=dy\) より、\(dx=\displaystyle\frac{dy}{f'(x)}\)
となりますが逆関数の微分を考えれば、\(f'(x)=\displaystyle\frac{dy}{dx}=\displaystyle\frac{1}{\displaystyle\frac{dx}{dy}}\)
なので、\(dx=\displaystyle\frac{dx}{dy}\cdot dy\) です。\(\displaystyle\frac{dx}{dy}\) は \(\sin y=x\) より簡単に求められ
\(\displaystyle\int f(x)dx=\displaystyle\int y(\sin y)’dy\) となります。あとは区間も変換するだけです。
\(x=\sin y\)・・・① \(⇔\) \(y=f(x)\)
\(I=\displaystyle\int_{0}^{\frac{\sqrt{3}}{2}}f(x)dx\) について
\(f(x)=y\) で置換すると、\(f'(x)dx=dy\) より
\(dx=\displaystyle\frac{dy}{f'(x)}=\displaystyle\frac{dx}{dy}\cdot dy\)
よって①より
\(dx=\cos ydy\)
また①より \(x:0 \to \displaystyle\frac{\sqrt{3}}{2}\) のとき \(y:0 \to \displaystyle\frac{π}{3}\) だから
\(I=\displaystyle\int_{0}^{\frac{\sqrt{3}}{2}}f(x)dx\)
\(=\displaystyle\int_{0}^{\frac{π}{3}}y \cos y dy\)
\(=[y\sin y]_{0}^{\frac{π}{3}}-\displaystyle\int_{0}^{\frac{π}{3}}\sin ydy\)
\(=\displaystyle\frac{π}{3}\cdot\displaystyle\frac{\sqrt{3}}{2}+[\cos y]_{0}^{\frac{π}{3}}\)
\(=\displaystyle\frac{\sqrt{3}}{6}π-\displaystyle\frac{1}{2}\)
(解法2)面積を考える
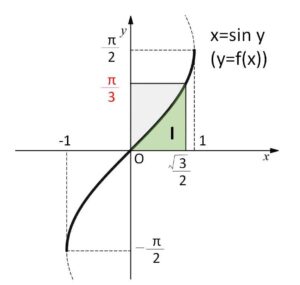
\(y=f(x)\) のグラフは、\(x=\sin y\) と同じ。また、\(x=\displaystyle\frac{\sqrt{3}}{2}\) に対応するのは \(y=\displaystyle\frac{π}{3}\)
よって図より
\(I=\displaystyle\int_{0}^{\frac{\sqrt{3}}{2}}f(x)dx\)
\(=\displaystyle\frac{\sqrt{3}}{2}\cdot\displaystyle\frac{π}{3}-\displaystyle\int_{0}^{\frac{π}{3}}\sin y dy\)
\(=\displaystyle\frac{\sqrt{3}}{6}π+[\cos y]_{0}^{\frac{π}{3}}\)
\(=\displaystyle\frac{\sqrt{3}}{6}π-\displaystyle\frac{1}{2}\)
(解法3)ダイレクトに部分積分する
\(x=\sin y\)・・・① \(⇔\) \(y=f(x)\)
\(I=\displaystyle\int_{0}^{\frac{\sqrt{3}}{2}}f(x)dx\) について
\(0≦x≦\displaystyle\frac{\sqrt{3}}{2}\) より \(0≦y≦\displaystyle\frac{π}{3}\) に注意して
\(f'(x)=\displaystyle\frac{dy}{dx}=\displaystyle\frac{1}{\displaystyle\frac{dx}{dy}}\)
\(=\displaystyle\frac{1}{\cos y}\) (①より)
\(=\displaystyle\frac{1}{\sqrt{1-x^2}}\) (\(\cos y>0\) より)
よって
\(I=\displaystyle\int_{0}^{\frac{\sqrt{3}}{2}}1\cdot f(x)dx\)
\(=[xf(x)]_{0}^{\frac{\sqrt{3}}{2}}-\displaystyle\int_{0}^{\frac{\sqrt{3}}{2}}\displaystyle\frac{x}{\sqrt{1-x^2}}dx\) (2項目は微分接触型)
\(=\displaystyle\frac{\sqrt{3}}{2}f(\displaystyle\frac{\sqrt{3}}{2})+[\sqrt{1-x^2}]_{0}^{\frac{\sqrt{3}}{2}}\)
(\(x=\displaystyle\frac{\sqrt{3}}{2}\) に対応するのは、\(y=\displaystyle\frac{π}{3}\))
\(=\displaystyle\frac{\sqrt{3}}{2}\cdot\displaystyle\frac{π}{3}+(\sqrt{\displaystyle\frac{1}{4}}-1)\)
\(=\displaystyle\frac{\sqrt{3}}{6}π-\displaystyle\frac{1}{2}\)
(例題2)
連続関数\(f(x)\)が、逆関数\(g(x)\)をもつとき、次の等式が成り立つことを示せ。
\(\displaystyle\int_{a}^{b}f(x)dx+\displaystyle\int_{f(a)}^{f(b)}g(x)dx=bf(b)-af(a)\)
(解答)
\(g(x)\)の積分の方を変形することにすると、\(y=g(x)\) と \(x=f(y)\) が全く同じ式であることには注意します。また逆関数についての公式
\(f(f^{-1}(x))=f^{-1}(f(x))=x\) を利用します。
なおグラフの形状や\(a,b\)の大小正負などが分からないので、面積による解法は参考に留めたいと思います。
\(S=\displaystyle\int_{f(a)}^{f(b)}g(x)dx\) について
\(y=g(x)\) で置換すると
\(y=g(x)\) \(⇔\) \(x=f(y)\) だから
\(dx=f'(y)dy\)
また、\(x:f(a) \to f(b)\) のとき \(y:g(f(a)) \to g(f(b))\)
つまり、\(y:a \to b\) だから
\(S=\displaystyle\int_{a}^{b}yf'(y)dy\)
(部分積分をして)
\(=[yf(y)]_{a}^{b}-\displaystyle\int_{a}^{b}f(y)dy\)
(積分変数を変えても変わらないので)
\(=bf(b)-af(a)-\displaystyle\int_{a}^{b}f(x)dx\)
したがって
\(\displaystyle\int_{a}^{b}f(x)dx+\displaystyle\int_{f(a)}^{f(b)}g(x)dx=bf(b)-af(a)\)
(参考)
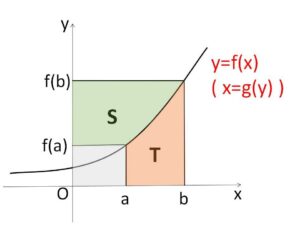
\(0<a<b\)、\(f(x)>0\) と限定して
\(S=\displaystyle\int_{f(a)}^{f(b)}g(x)dx\ (=\displaystyle\int_{f(a)}^{f(b)}g(y)dy)\) (変数を変えただけ)
\(T=\displaystyle\int_{a}^{b}f(x)dx\) とおけば
\(T+S=bf(b)-af(a)\)
が成り立つことが視覚的も分かります。
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→逆関数と定積分② back→e,πが無理数であることの証明