最終的に区分求積法を利用する極限の例題です。
(例題1)
座標平面上に原点\(O\)を中心とする半径\(1\)の円\(C\)がある。点\(A(-2,0)\)を通る直線が \(y>0\) の範囲にある点\(P\)において円\(C\)と接するとする。自然数 \(n≧2\) に対して点\(A\) を通る\((n-1)\)本の直線で \(\angle OAP\) を\(n\)等分する。これらの直線を直線\(AO\)となす角が小さいものから順に \(l_1,\cdots,l_{n-1}\) とし、直線\(l_k\)と円\(C\)の2つの交点のうち点\(A\)に近い方を\(Q_k\)、他方を\(R_k\)とする。
(1)\(AR_k^2-AQ_k^2\) を\(n\)と\(k\)を用いて表せ。
(2)極限値 \(\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n-1}(AR_k^2-AQ_k^2)\) を求めよ。
(解答)
(1)
\(△OAP\)は、辺の長さが \(1:2:\sqrt{3}\) の直角三角形なので、\(\angle OAP=\displaystyle\frac{π}{6}\) です。よって \(\angle OAQ_k\ (\angle OAR_k)=\displaystyle\frac{π}{6}\cdot\displaystyle\frac{k}{n}\) です。
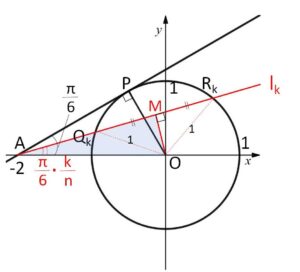
図より
\(OM=2\sin\displaystyle\frac{kπ}{6n}\) だから
\(MQ_k=MR_k=\sqrt{1-4\sin^2\displaystyle\frac{kπ}{6n}}\)
また、\(AM=2\cos\displaystyle\frac{kπ}{6n}\) より
\(AQ_k=2\cos\displaystyle\frac{kπ}{6n}-\sqrt{1-4\sin^2\displaystyle\frac{kπ}{6n}}\)
\(AR_k=2\cos\displaystyle\frac{kπ}{6n}+\sqrt{1-4\sin^2\displaystyle\frac{kπ}{6n}}\)
よって
\(AR_k^2-AQ_k^2\)
\(=8\cos\displaystyle\frac{kπ}{6n}\sqrt{1-4\sin^2\displaystyle\frac{kπ}{6n}}\)
(2)
積分は導関数接触型になります。
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n-1}(AR_k^2-AQ_k^2)\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n-1}8\cos(\displaystyle\frac{π}{6}\cdot\displaystyle\frac{k}{n})\sqrt{1-4\sin^2(\displaystyle\frac{π}{6}\cdot\displaystyle\frac{k}{n})}\)
\(=\displaystyle\int_{0}^{1}8\cos\displaystyle\frac{π}{6}x\sqrt{1-4\sin^2\displaystyle\frac{π}{6}x}\ dx\)・・・①
\(\sin\displaystyle\frac{π}{6}x=t\) とおくと
\(\displaystyle\frac{π}{6}\cos\displaystyle\frac{π}{6}x\ dx=dt\) だから
①\(=\displaystyle\int_{0}^{\frac{1}{2}}8\sqrt{1-4t^2}\cdot\displaystyle\frac{6}{π} dt\)
\(=\displaystyle\frac{48}{π}\displaystyle\int_{0}^{\frac{1}{2}}\sqrt{4(\displaystyle\frac{1}{4}-t^2)}dt\)
\(=\displaystyle\frac{96}{π}\displaystyle\int_{0}^{\frac{1}{2}}\sqrt{\displaystyle\frac{1}{4}-t^2}dt\)
(半径\(\displaystyle\frac{1}{2}\)の円の\(\displaystyle\frac{1}{4}\)の面積)
\(=\displaystyle\frac{96}{π}\cdot(\displaystyle\frac{1}{2})^2π\cdot\displaystyle\frac{1}{4}\)
\(=6\)
(例題2)
\(n\)個のボールを\(2n\)個の箱へ投げ入れる。各ボールはいずれかの箱に入るものとし、どの箱に入る確率も等しいとする。どの箱にも1個以下のボールしか入っていない確率を\(p_n\)とする。このとき、極限値 \(\displaystyle\lim_{n \to \infty}\displaystyle\frac{\log p_n}{n}\) を求めよ。
(解答)
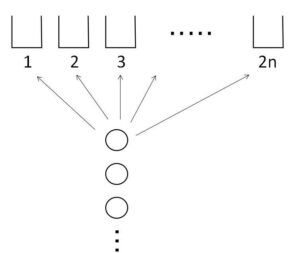
1つのボールの入れ方は\(2n\)通り。どの箱にも1個以下のボールしか入っていない確率\(p_n\)は、
\(p_n=\displaystyle\frac{2n}{2n}\cdot\displaystyle\frac{2n-1}{2n}\cdot\displaystyle\frac{2n-2}{2n}\cdots\displaystyle\frac{n+1}{2n}\)
(積は\(n\)個。最後は \(2n-n+1=n+1\) になる)
よって
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{\log p_n}{n}\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\log\left(\displaystyle\frac{2n}{2n}\cdot\displaystyle\frac{2n-1}{2n}\cdot\displaystyle\frac{2n-2}{2n}\cdots\displaystyle\frac{n+1}{2n}\right)\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\log\left(\displaystyle\frac{n+n}{2n}\cdot\displaystyle\frac{n+(n-1)}{2n}\cdot\displaystyle\frac{n+(n-2)}{2n}\cdots\displaystyle\frac{n+1}{2n}\right)\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\log\left(\displaystyle\frac{1}{2}+\displaystyle\frac{n}{2n}\right)\left(\displaystyle\frac{1}{2}+\displaystyle\frac{n-1}{2n}\right)\left(\displaystyle\frac{1}{2}+\displaystyle\frac{n-2}{2n}\right)\cdots\left(\displaystyle\frac{1}{2}+\displaystyle\frac{1}{2n}\right)\)
(\(\log\)の真数の積は和になるから)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\log(\displaystyle\frac{1}{2}+\displaystyle\frac{k}{2n})\)
\(=\displaystyle\int_{0}^{1}\log(\displaystyle\frac{1}{2}+\displaystyle\frac{1}{2}x)dx\)
\(=\displaystyle\int_{0}^{1}\log\displaystyle\frac{1+x}{2}dx\)
\(=\displaystyle\int_{0}^{1}\{\log(1+x)-\log2\}dx\)
(部分積分)
\(=[(1+x)\log(1+x)]_{0}^{1}-\displaystyle\int_{0}^{1}dx-(\log2)[x]_{0}^{1}\)
\(=2\log2-[x]_{0}^{1}-\log2\)
\(=\log2-1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→定積分と不等式① back→区分求積法②