定積分と不等式②(三角形・台形近似)

三角形や台形の面積により定積分を評価する例題です。

(例題1)
(1)\(0≦x≦\displaystyle\frac{π}{2}\) のとき、次の不等式を証明せよ。
\(\displaystyle\frac{2}{π}x≦\sin x\)

(2)次の不等式を証明せよ。
\(\displaystyle\frac{π}{2}(e-1)<\displaystyle\int_{0}^{\frac{π}{2}}e^{\sin x}dx<e^{\frac{π}{2}}-1\)

(解答)
(1)

\(f(x)=\sin x-\displaystyle\frac{2}{π}x\)　(\(0≦x≦\displaystyle\frac{π}{2}\))
とおく。

\(f'(x)=\cos x-\displaystyle\frac{2}{π}\)

ここで、\(0<\displaystyle\frac{2}{π}<1\) より
\(\cos x=\displaystyle\frac{2}{π}\) を満たす\(x\)が範囲の中にただ1つ存在し、それを\(c\) (\(0<c<\displaystyle\frac{π}{2}\)) とおくと、増減表は次の通り。

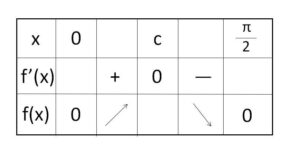
よって \(f(x)≧0\) となるから
\(\displaystyle\frac{2}{π}x≦\sin x\)　(\(0≦x≦\displaystyle\frac{π}{2}\) )

※グラフで考えると

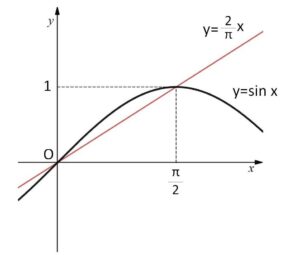
\(y=\sin x\) が \(0<x≦\displaystyle\frac{π}{2}\) で上に凸の関数なので、\(y=\displaystyle\frac{2}{π}x\) は下側にあります。この位置関係からも不等式が成り立つことが分かります。

(2)

\(\displaystyle\int_{0}^{\frac{π}{2}}e^{\sin x}dx\) は計算できないので、計算しやすい定積分を使って不等式ではさみこみます。もちろん(1)の不等式は使いますが、もう片側については \(y=\sin x\) の接線を利用します。\(y=\sin x\) が \(0<x≦\displaystyle\frac{π}{2}\) で上に凸の関数なので、接線は上側にあります(解答では(1)と同様に微分して示します)。
なお、この例題では直接使いませんが、定積分を三角形の面積ではさみこむという方法は非常によく使います。

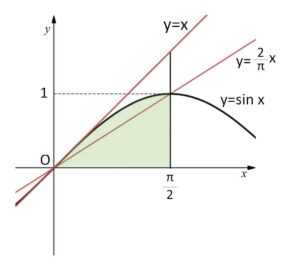
\(y=\sin x\) を微分すると \(y’=\cos x\) だから
原点における \(y=\sin x\) の接線は \(y=x\)

そこでまず
\(\sin x≦x\)　(\(0≦x≦\displaystyle\frac{π}{2}\))
を示す。

\(g(x)=x-\sin x\)　(\(0≦x≦\displaystyle\frac{π}{2}\))
とおくと
\(g'(x)=1-\cos x≧0\)

よって、\(g(x)\)は単調増加関数で、\(g(0)=0\) より
\(g(x)≧0\)
ゆえに \(\sin x≦x\) が成り立つ。

(1)の結果も合わせると
\(\displaystyle\frac{2}{π}x≦\sin x≦x\)・・・①

ゆえに
\(e^{\frac{2}{π}x}≦e^{\sin x}≦e^{x}\)・・・②

①の等号は \(0≦x≦\displaystyle\frac{π}{2}\) の範囲では常には成り立たないので②も同様に成り立たない。したがって②より

\(\displaystyle\int_{0}^{\frac{π}{2}}e^{\frac{2}{π}x}dx<\displaystyle\int_{0}^{\frac{π}{2}}e^{\sin x}dx<\displaystyle\int_{0}^{\frac{π}{2}}e^{x}dx\)

\(\left[\displaystyle\frac{π}{2}e^{\frac{2}{π}x}\right]_{0}^{\frac{π}{2}}<\displaystyle\int_{0}^{\frac{π}{2}}e^{\sin x}dx<[e^{x}]_{0}^{\frac{π}{2}}\)

\(\displaystyle\frac{π}{2}(e-1)<\displaystyle\int_{0}^{\frac{π}{2}}e^{\sin x}dx<e^{\frac{π}{2}}-1\)

(例題2)
\(f(x)=\displaystyle\frac{1}{1+x^2}\) とし、曲線 \(y=f(x)\) (\(x>0\)) の変曲点を \((a,f(a))\) とする。

(1)\(a\)の値を求めよ。
(2)\(I=\displaystyle\int_{a}^{1}f(x)dx\) の値と、4点 \((a,f(a))\)、\((a,0)\)、\((1,0)\)、\((1,f(1))\) を頂点とする台形の面積\(S\)を求めよ。
(3)円周率\(π\)は\(3.17\)より小さいことを証明せよ。ただし必要ならば \(\sqrt{3}>1.732\) を用いてよい。

(解答)

(1)
\(f(x)=\displaystyle\frac{1}{1+x^2}\)　(\(x>0\))　より

\(f'(x)=\displaystyle\frac{-2x}{(1+x^2)^2}\)

\(f”(x)=\displaystyle\frac{-2(1+x^2)^2+2x\cdot2(1+x^2)\cdot2x}{(1+x^2)^4}\)

\(=\displaystyle\frac{2(3x^2-1)}{(1+x^2)^3}\)

よって \(x=\displaystyle\frac{1}{\sqrt{3}}\) 前後で\(f”(x)\)の符号が変わるので
変曲点は \((\displaystyle\frac{1}{\sqrt{3}},\displaystyle\frac{3}{4})\)

したがって \(a=\displaystyle\frac{1}{\sqrt{3}}\)

(2)
(定積分は \(x=\tanθ\) の置換をする基本パターンです)

\(x=\tanθ\) と置換すると

\(I=\displaystyle\int_{\frac{1}{\sqrt{3}}}^{1}\displaystyle\frac{1}{x^2+1}dx\)

\(=\displaystyle\int_{\frac{π}{6}}^{\frac{π}{4}}\displaystyle\frac{1}{\tan^2θ+1}\cdot\displaystyle\frac{1}{\cos^2θ}dθ\)

\(=\displaystyle\int_{\frac{π}{6}}^{\frac{π}{4}}dθ\)

\(=\displaystyle\frac{π}{4}-\displaystyle\frac{π}{6}\)

\(=\displaystyle\frac{π}{12}\)

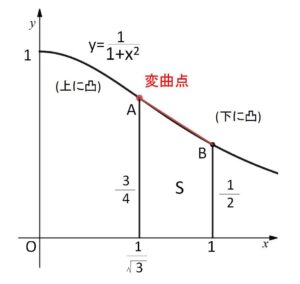
また、台形の面積\(S\)については、4点が \((\displaystyle\frac{1}{\sqrt{3}},\displaystyle\frac{3}{4})\)、\((\displaystyle\frac{1}{\sqrt{3}},0)\)、\((1,0)\)、\((1,\displaystyle\frac{1}{2})\) となるので

\(S=\displaystyle\frac{1}{2}(\displaystyle\frac{1}{2}+\displaystyle\frac{3}{4})(1-\displaystyle\frac{1}{\sqrt{3}})\)

\(=\displaystyle\frac{5(3-\sqrt{3})}{24}\)

(3)

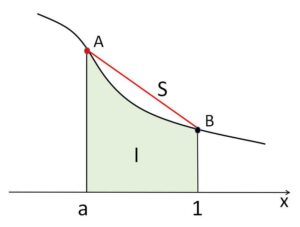
\(x>a\) において \(y=f(x)\) のグラフは下に凸なので、台形の辺\(AB\)はグラフの上側にある。
よって台形の面積のほうが大きいから、\(S>I\)

(1)(2)より
\(\displaystyle\frac{5(3-\sqrt{3})}{24}>\displaystyle\frac{π}{12}\) となるから

\(π<\displaystyle\frac{5(3-\sqrt{3})}{2}<\displaystyle\frac{5(3-1.732)}{2}=3.17\)　(\(-\sqrt{3}<-1.732\) より)

したがって
\(π<3.17\)

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→積分型の平均値の定理　back→定積分と不等式①