積分型の平均値の定理

積分型の平均値の定理について見ていきます。

・積分型の平均値の定理

形式が平均値の定理(微分型)と同じなので、積分の平均値の定理と呼ばれます。
存在することを保証する定理なので、その\(c\)の個数は問いません。(2個以上あることもある)

証明は、微分型の平均値の定理を利用する方法と、連続関数であることから最大値・最小値の定理と中間値の定理を利用する方法を紹介します。

(証明1)微分型の平均値の定理を利用

\(f(x)\) の原始関数の1つを \(F(x)\) として

\(F(x)=\displaystyle\int_{a}^{x}f(x)dx\)

とおく。すると \(F(x)\) は連続 (\(f(x)\)が連続だから、面積が連続的に変化する) で \(F'(x)=f(x)\) を満たすので、平均値の定理(微分型)より

\(\displaystyle\frac{F(b)-F(a)}{b-a}=f(c)\)　(\(a<c<b\))

を満たす\(c\)が存在する。よって

\(\displaystyle\int_{a}^{b}f(x)dx=(b-a)f(c)\)　(\(a<c<b\))

を満たす\(c\)が存在する。

(証明2)最大値・最小値の定理を利用
\(f(x)\)は \(a≦x≦b\) で連続関数なので、この区間で最大値と最小値をもつ。

(ア)\(f(x)\)が定数関数の場合(最大値と最小値が同じ)
区間内で常に \(f(x)=k\) だから
\(\displaystyle\int_{a}^{b}f(x)dx=\displaystyle\int_{a}^{b}k dx=k(b-a)\)

よって
\(\displaystyle\int_{a}^{b}f(x)dx=(b-a)f(c)\)　(\(a<c<b\))を満たす\(c\)が存在する。(無数にある)

(イ)\(f(x)\)が定数関数でない場合
区間内で最大値\(M\)と最小値\(m\) (\(m<M\)) をもつ。そのときの\(x\)の値を\(x_1,x_2\)とすると、\(f(x_1)=M\)、\(f(x_2)=m\)

すると、\(m≦f(x)≦M\) で、等号は常には成り立たないので
\(\displaystyle\int_{a}^{b}mdx<\displaystyle\int_{a}^{b}f(x)dx<\displaystyle\int_{a}^{b}Mdx\)

よって
\(m(b-a)<\displaystyle\int_{a}^{b}f(x)dx<M(b-a)\)

\(b>a\) だから
\(m<\displaystyle\frac{1}{b-a}\displaystyle\int_{a}^{b}f(x)dx<M\)

(\(I=\displaystyle\frac{1}{b-a}\displaystyle\int_{a}^{b}f(x)dx\)・・・① とおく)

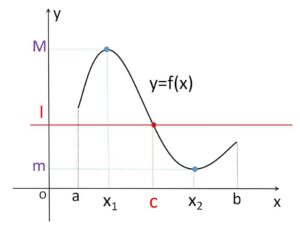
\(I\)は\(M\)と\(m\)の間の値であり、\(f(x)\)は連続関数で\(f(x_1)≠f(x_2)\) (\(M≠m\)) だから、中間値の定理より
\(f(c)=I\)・・・②
を満たす\(c\)が、\(x_1\)と\(x_2\)の間に存在する。

したがって①②より
\(\displaystyle\frac{1}{b-a}\displaystyle\int_{a}^{b}f(x)dx=f(c)\)　(\(a<c<b\))

を満たす\(c\)が存在する。(\(c\)は\(x_1\)と\(x_2\)の間にあるから、\(a\)と\(b\)の間にある)

(例題)
\(a\)を定数、\(n\)を自然数とする。
\(I_n=\displaystyle\int_{a}^{a+\frac{1}{n}}x\cos^2(x-a)dx\)
とするとき、\(\displaystyle\lim_{n \to \infty}nI_n\) を求めよ。(積分の平均値の定理を利用せよ)

(解答)
\(f(x)=x\cos^2(x-a)\) は連続関数なので

\(\displaystyle\int_{a}^{a+\frac{1}{n}}x\cos^2(x-a)dx=(a+\displaystyle\frac{1}{n}-a)\cdot c\cos^2(c-a)\)・・・①
(\(a<c<a+\displaystyle\frac{1}{n}\)・・・②)

を満たす\(c\)が存在する。

①より
\(I_n=\displaystyle\frac{1}{n}\cdot c\cos^2(c-a)\) だから

\(nI_n=c\cos^2(c-a)\)

また②より \(n \to \infty\) のとき \(c \to a\) だから

\(\displaystyle\lim_{n \to \infty}nI_n=\displaystyle\lim_{c \to a}c\cos^2(c-a)\)

\(=a\cos^20\)

\(=a\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→積分型のシュワルツの不等式　back→定積分と不等式②