定積分に関する極限の例題です。
①グラフで囲まれる面積を長方形の短冊等の面積と比較する。
②グラフの大小から、定積分の大小を導く。
これらは定積分が計算できない場合に特に有効ですが、逆に定積分が計算できる場合に、和の方を定積分で評価する場合もあります。
いずれも最終的な決め手ははさみうちの原理です。
(例題1)
\(n\)は\(2\)以上の自然数とする。
(1)\(x>0\) のとき、\(\log x<\sqrt{x}\) を示せ。
(2)\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{\log x}{x}=0\) を示せ。
(3)\(\displaystyle\int_{1}^{n}\log xdx<\log(n!)<\displaystyle\int_{1}^{n+1}\log xdx\) を示せ。
(4)\(a_n=\left(\displaystyle\frac{n!}{n^{n}}\right)^{\frac{1}{n}}\) とするとき、\(\displaystyle\lim_{n \to \infty}a_n=\displaystyle\frac{1}{e}\) を示せ。
(解答)
(1)
\(f(x)=\sqrt{x}-\log x\) (\(x>0\))とおく。
\(f'(x)=\displaystyle\frac{1}{2\sqrt{x}}-\displaystyle\frac{1}{x}\)\(=\displaystyle\frac{\sqrt{x}-2}{2x}\)
よって
\(x=4\) のとき \(f(x)\) は最小値 \(f(4)=2-\log 4=2(\log e-\log 2)\ (>0)\) をとる。
したがって \(f(x)>0\) だから
\(\log x<\sqrt{x}\) (\(x>0\))
が成り立つ。
(2)
\(x \to \infty\) より、\(x\)は十分大きい正の数としてよく、(1)より
\(0<\log x<\sqrt{x}\)
\(x\)で辺々割ると
\(0<\displaystyle\frac{\log x}{x}<\displaystyle\frac{1}{\sqrt{x}}\)
よってはさみうちの原理より
\(\displaystyle\lim_{x \to \infty}\displaystyle\frac{\log x}{x}=0\)
(3)
\(\log(n!)=\log1+\log2+\cdots+\log n\)
より、長方形の短冊の面積と定積分を比較すればうまくいきそうです。
最初から全体の長方形の短冊の面積の和を考えてもよいですが、今回は1つの長方形の面積についてまず考える方法を取りたいと思います。
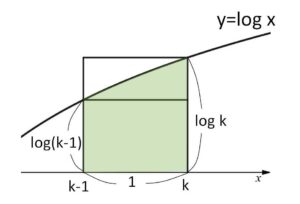
\(k=2,3,\cdots\) のとき、図より
\(1\cdot\log(k-1)<\displaystyle\int_{k-1}^{k}\log x dx<1\cdot\log k\)・・・①
①の右辺で、\(k=2,3,\cdots,n\) まで変化させて辺々加えると
\(\displaystyle\int_{1}^{2}\log xdx+\displaystyle\int_{2}^{3}\log xdx+\cdots+\displaystyle\int_{n-1}^{n}\log xdx<\log2+\log3+\cdots+\log n\)
よって \(\log 1=0\) であることも踏まえると
\(\displaystyle\int_{1}^{n}\log xdx<\log(n!)\)・・・②
同様に①の左辺で、\(k=2,3,\cdots,n+1\) まで変化させて辺々加えると
\(\log1+\log2+\cdots+\log n<\displaystyle\int_{1}^{2}\log xdx+\displaystyle\int_{2}^{3}\log xdx+\cdots+\displaystyle\int_{n}^{n+1}\log xdx\)
よって
\(\log(n!)<\displaystyle\int_{1}^{n+1}\log xdx\)・・・③
②③より
\(\displaystyle\int_{1}^{n}\log xdx<\log(n!)<\displaystyle\int_{1}^{n+1}\log xdx\)
(4)
\(\log\left(\displaystyle\frac{n!}{n^{n}}\right)^{\frac{1}{n}}=\displaystyle\frac{\log(n!)-n\log n}{n}\)
なので、この形を目指します。(3)の両側の定積分は計算できるので求めておきます。
(3) より
\(\displaystyle\int_{1}^{n}\log xdx<\log(n!)<\displaystyle\int_{1}^{n+1}\log xdx\)
\(\displaystyle\int \log xdx=x\log x-x+C\) なので (部分積分を用いた)
\(n\log n-n+1<\log(n!)<(n+1)\log(n+1)-(n+1)+1\)
辺々 \(n\log n\) を引いて、\(n\)で割ると
\(-1+\displaystyle\frac{1}{n}<\displaystyle\frac{\log(n!)-n\log n}{n}<(1+\displaystyle\frac{1}{n})\log(n+1)-1-\log n\)
右辺を整理すると
\(-1+\displaystyle\frac{1}{n}<\displaystyle\frac{\log(n!)-n\log n}{n}<\log\displaystyle\frac{n+1}{n}+\displaystyle\frac{\log(n+1)}{n}-1\)
((2)の極限が使えるようにする)
\(-1+\displaystyle\frac{1}{n}<\displaystyle\frac{\log(n!)-n\log n}{n}<\log\displaystyle\frac{n+1}{n}+\displaystyle\frac{\log(n+1)}{n+1}\cdot\displaystyle\frac{n+1}{n}-1\)
よって\(n \to \infty\) のとき
(左辺)\(\to -1\)
(右辺)\(\to \log1+0\cdot1-1=-1\)
だから、はさみうちの原理より
\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{\log(n!)-n\log n}{n}=-1\)・・・④
\(\displaystyle\frac{\log(n!)-n\log n}{n}=\displaystyle\frac{\log(n!)-\log n^n}{n}\)
\(=\displaystyle\frac{1}{n}\log\left(\displaystyle\frac{n!}{n^n}\right)=\log\left(\displaystyle\frac{n!}{n^n}\right)^{\frac{1}{n}}\) だから④より
\(\displaystyle\lim_{n \to \infty}\log\left(\displaystyle\frac{n!}{n^n}\right)^{\frac{1}{n}}=\log e^{-1}\)
したがって
\(\displaystyle\lim_{n \to \infty}\left(\displaystyle\frac{n!}{n^n}\right)^{\frac{1}{n}}=\displaystyle\frac{1}{e}\)
(例題2)
\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{\frac{1}{2}}\displaystyle\frac{x^n}{1-x}dx\) を求めよ。
積分区間が \(0≦x≦\displaystyle\frac{1}{2}\) であることと、\(n\) を残すことを意識して、\(1-x\) のほうをいじります(この問題だと\(1-x\)のほうを残しても解けますが)。\(\displaystyle\frac{1}{2}≦1-x≦1\) なので、
\(1≦\displaystyle\frac{1}{1-x}≦2\) です。よって
\(x^n≦\displaystyle\frac{x^n}{1-x}≦2x^n\) が成り立ちます。
(解答)
\(0≦x≦\displaystyle\frac{1}{2}\)・・・① において
\(1≦\displaystyle\frac{1}{1-x}≦2\) だから
\(x^{n}≦\displaystyle\frac{x^n}{1-x}≦2x^{n}\)
よって
\(\displaystyle\int_{0}^{\frac{1}{2}}x^{n}dx≦\displaystyle\int_{0}^{\frac{1}{2}}\displaystyle\frac{x^n}{1-x}dx≦\displaystyle\int_{0}^{\frac{1}{2}}2x^{n}dx\) (等号を抜いてもよい)
\(\left[\displaystyle\frac{x^{n+1}}{n+1}\right]_{0}^{\frac{1}{2}}≦\displaystyle\int_{0}^{\frac{1}{2}}\displaystyle\frac{x^n}{1-x}dx≦\left[\displaystyle\frac{2x^{n+1}}{n+1}\right]_{0}^{\frac{1}{2}}\)
\(\displaystyle\frac{1}{2^{n+1}(n+1)}≦\displaystyle\int_{0}^{\frac{1}{2}}\displaystyle\frac{x^n}{1-x}dx≦\displaystyle\frac{1}{2^{n}(n+1)}\)
したがってはさみうちの原理より
\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{\frac{1}{2}}\displaystyle\frac{x^n}{1-x}dx=0\)
\(0≦\displaystyle\int_{0}^{\frac{1}{2}}\displaystyle\frac{x^n}{1-x}dx≦\cdots\)
としてもよいです。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→ガウス記号と定積分 back→積分型のシュワルツの不等式