回転体の体積は、断面積を考えて積分することで求めることができます。
・回転体の体積
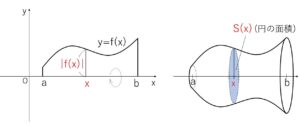
曲線 \(y=f(x)\) と \(x\)軸, 2直線 \(x=a\), \(x=b\) (\(a<b\)) で囲まれた部分を\(x\)軸の周りに1回転してできる体積を\(V\)とします。
点\((x,0)\)を通り\(x\)軸に垂直な平面\(γ\)で立体を切断することを考えると、この断面の回転前の図形は、長さ \(|f(x)|\) の線分だから、断面図は半径\(|f(x)|\)の円になります。
よって、平面\(γ\)による断面積は、\(S(x)=π\{f(x)\}^2=πy^2\) となるから
\(V=π\displaystyle\int_{a}^{b}\{f(x)\}^2dx=π\displaystyle\int_{a}^{b}y^2dx\)
また、\(y\)軸周りの回転も同様に
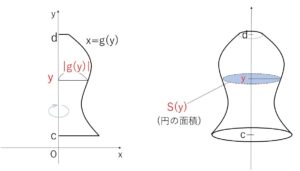
曲線 \(x=g(y)\) と \(y\)軸, 2直線 \(y=c\), \(y=d\) (\(c<d\)) で囲まれた部分を\(y\)軸の周りに1回転してできる体積を\(V_y\)とすると
\(V_y=π\displaystyle\int_{c}^{d}\{g(y)\}^2dy=π\displaystyle\int_{c}^{d}x^2dy\)
①符号が同じだと、面積のときと同じように2つの回転体の体積の差を考える
②符号が反対だと、重複する部分がでてくるので絶対値の大きいほうの関数を優先する
ことになります。詳しくは次回の例題で扱います。
(例題1)積分を用いて次の立体の体積を求めよ。
(1)底面の半径\(r\),高さ\(h\)の直円錐の体積
(2)底面積\(S\)、高さ\(h\)の正三角錐 および 正四角錐の体積
(3)半径\(r\)の球の体積
(解答)
(1)
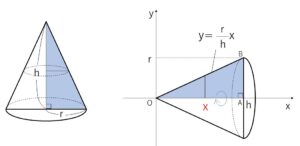
図のように直角三角形\(OAB\)を座標平面に設定すると、円錐は\(△OAB\)を\(x\)軸周りに回転させたものになる。
直線\(OA\)の方程式は
\(y=\displaystyle\frac{r}{h}x\) だから、体積\(V\)は
\(V=π\displaystyle\int_{0}^{h}(\displaystyle\frac{r}{h}x)^2dx\)
\(=\displaystyle\frac{πr^2}{h^2}\left[\displaystyle\frac{x^3}{3}\right]_0^h\)
\(=\displaystyle\frac{1}{3}πr^2h\)
(2)
(1)についても同様に比を考えても解くことができます。
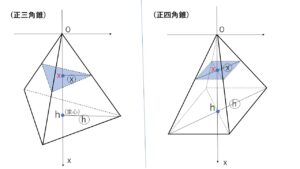
(正三角錐)
図のように\(x\)軸を設定し、\(x\)座標が\(x\)であるときの断面積を\(S(x)\)とすると、
底面との相似比が \(h:x\) であることから
\(S:S(x)=h^2:x^2\)
よって
\(S(x)=\displaystyle\frac{x^2}{h^2}S\) より体積\(V\)は
\(V=\displaystyle\int_{0}^{h}(\displaystyle\frac{x^2}{h^2}S)dx\)
\(=\displaystyle\frac{S}{h^2}\left[\displaystyle\frac{1}{3}x^3\right]_{0}^{h}\)
\(=\displaystyle\frac{1}{3}Sh\)
(正四角錐)
正三角錐のときと同様に、底面との相似比を考えると
\(S(x)=\displaystyle\frac{x^2}{h^2}S\) より体積\(V\)は
\(V=\displaystyle\int_{0}^{h}(\displaystyle\frac{x^2}{h^2}S)dx\)
\(=\displaystyle\frac{S}{h^2}\left[\displaystyle\frac{1}{3}x^3\right]_{0}^{h}\)
\(=\displaystyle\frac{1}{3}Sh\)
(3)
積分計算する際には、直径を座標平面の\(x\)軸に一致させて考えると分かりやすいです。
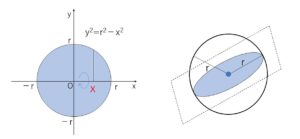
円 \(x^2+y^2=r^2\) を \(x\)軸回りに回転させると半径\(r\)の球になるので体積\(V\)は
\(V=π\displaystyle\int_{-r}^{r}y^2dx\)
\(=π\displaystyle\int_{-r}^{r}(r^2-x^2)dx\)
\(=2π\left[r^2x-\displaystyle\frac{1}{3}x^3\right]_{0}^{r}\)
\(=\displaystyle\frac{4}{3}πr^3\)
(例題2)
半径が\(4,5\)である2つの球の中心間の距離が\(3\)である。この2つの球の共通部分の体積を求めよ。
半径\(4,5\)の2円が中心間距離\(3\)になるように配置させて、この共通部分の回転体の体積を考えます。(2つの球の中心を両方通るような平面で切った時の断面図になる)
(解答)
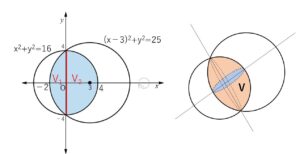
2つの円①②の周および内部の共通部分を、\(x\)軸回りに回転してできた立体の体積が球の共通部分の体積\(V\)になる。
\(x^2+y^2=16\)・・・①
\((x-3)^2+y^2=25\)・・・②
①-②より
\(6x-9=-9\)
\(x=0\)
①より \(y=±4\)
(2円の交点は \((0,±4)\)
分けて考えて、\(V=V_1+V_2\) を求めます。
したがって体積\(V\)は
\(V=π\displaystyle\int_{-2}^{0}\{25-(x-3)^2\}dx+π\displaystyle\int_{0}^{4}(16-x^2)dx\)
\(=π\left[25x-\displaystyle\frac{(x-3)^3}{3}\right]_{-2}^{0}+π\left[16x-\displaystyle\frac{1}{3}x^3\right]_{0}^{4}\)
\(=9π-(-50+\displaystyle\frac{125}{3})π+64π-\displaystyle\frac{64}{3}π\)
\(=60π\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→回転体の体積② back→定積分と体積の関係