内外サイクロイドと面積の例題です。
(例題1)
座標平面上の原点\(O\)を中心とする半径\(4\)の定円\(C_1\)に半径\(1\)の円\(C_2\)が外接しながらすべらずに反時計回りに回転する。円\(C_2\)の周上に点\(P\)が固定されている。\(C_2\)の中心\(Q\)が点\((5,0)\)にあるとき、点\(P\)はちょうど円\(C_1\)と\(C_2\)の接点\((4,0)\)の位置にあるものとする。\(C_2\)の中心\(Q\)が点\((5,0)\)の位置から点\((0,5)\)の位置まで進むとき、点\(P\)の描く曲線を\(C\)とする。
(1)\(x\)軸の正の方向と線分\(OQ\)のなす角を\(θ\) (\(0≦θ≦\displaystyle\frac{π}{2}\)) とするとき、\(P\)の座標は \((5\cosθ-\cos5θ,\ 5\sinθ-\sin5θ)\) で与えられることを示せ。
(2)\(C\)上の点で\(x\)座標が最も大きくなる点を求めよ。
(3)曲線\(C\)と\(x\)軸、\(y\)軸で囲まれた部分の面積を求めよ。
(解答)
(1)
まずは\(P\)の媒介変数表示をしますが、等しい長さの円弧に着目してベクトルを利用して求めます。等しい長さの円弧については、固定された円周に塗料が塗ってあるとして、転がった分だけ円に塗料が付くと考えるとよいです。
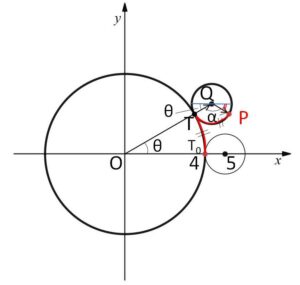
図のように点と角を設定する。
\(\stackrel{\huge\frown}{T_0T}=\stackrel{\huge\frown}{TP}\) だから
\(4θ=1α\)
よって \(α=4θ\)
\(Q\)を通る\(x\)軸に平行な線分を考えると
\(\overrightarrow{QP}=(\cos(-π+θ+α),\ \sin(-π+θ+α) )\)
\(=(-\cos(θ+α),-\sin(θ+α))\)
\(=(-\cos5θ,-\sin5θ)\)
したがって
\(\overrightarrow{OP}=\overrightarrow{OQ}+\overrightarrow{QP}\)
\(=(5\cosθ,5\sinθ)+(-\cos5θ,-\sin5θ)\)
\(=(5\cosθ-\cos5θ,5\sinθ-\sin5θ)\)
となるから
\(P(5\cosθ-\cos5θ,5\sinθ-\sin5θ)\)
(2)
\(x=5\cosθ-\cos5θ\) (\(0≦θ≦\displaystyle\frac{π}{2}\)) より
\(\displaystyle\frac{dx}{dθ}=-5\sinθ+5\sin5θ\)
\(=5(\sin5θ-\sinθ)\)
(和積より)
\(=10\cos3θ\sin2θ\)
\(0≦2θ≦π\) だから \(\sin2θ≧0\)
よって \(0≦3θ≦\displaystyle\frac{3}{2}π\) より
\(3θ=\displaystyle\frac{π}{2}\) のとき \(x\) は最大値をとる。
このとき、\(θ=\displaystyle\frac{π}{6}\) だから\(P\)の座標は
\(P(5\cos\displaystyle\frac{π}{6}-\cos\displaystyle\frac{5}{6}π,5\sin\displaystyle\frac{π}{6}-\sin\displaystyle\frac{5}{6}π)\)
\(=(\displaystyle\frac{5\sqrt{3}}{2}+\displaystyle\frac{\sqrt{3}}{2},\displaystyle\frac{5}{2}-\displaystyle\frac{1}{2})\)
\(=(3\sqrt{3},2)\)
(3)
\(y\)の正負も確認しておきます。
\(y=5\sinθ-\sin5θ\) (\(0≦θ≦\displaystyle\frac{π}{2}\))
\(\displaystyle\frac{dy}{dθ}=5\cosθ-5\cos5θ\)
\(=5(\cosθ-\cos5θ)\)
\(=10\sin3θ\sin2θ\)
よって
\(0<3θ<π\) のとき \(\displaystyle\frac{dy}{dθ}>0\)
\(π<3θ<\displaystyle\frac{3}{2}π\) のとき \(\displaystyle\frac{dy}{dθ}<0\)
\(θ=0\) のとき \(y=0\)
\(θ=\displaystyle\frac{π}{2}\) のとき \(y=4\)
となるから、\(y≧0\)
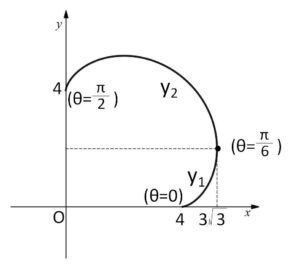
したがって面積\(S\)は \(dx=5(\sin5θ-\sinθ)dθ\) だから
\(S=\displaystyle\int_{0}^{3\sqrt{3}}y_2dx-\displaystyle\int_{4}^{3\sqrt{3}}y_1dx\)
\(=\displaystyle\int_{\frac{π}{2}}^{\frac{π}{6}}(5\sinθ-\sin5θ)\cdot5(\sin5θ-\sinθ)dθ-\displaystyle\int_{0}^{\frac{π}{6}}(5\sinθ-\sin5θ)\cdot5(\sin5θ-\sinθ)dθ\)
(積分区間をつなげるために変形。被積分関数は同じにする)
\(=5\displaystyle\int_{\frac{π}{6}}^{\frac{π}{2}}(5\sinθ-\sin5θ)(\sinθ-\sin5θ)dθ+5\displaystyle\int_{0}^{\frac{π}{6}}(5\sinθ-\sin5θ)(\sinθ-5\sinθ)dθ\)
\(=5\displaystyle\int_{0}^{\frac{π}{2}}(5\sinθ-\sin5θ)(\sinθ-\sin5θ)dθ\)
\(=5\displaystyle\int_{0}^{\frac{π}{2}}(5\sin^2θ-6\sin5θ\sinθ+\sin^25θ)dθ\)
\(=5\displaystyle\int_{0}^{\frac{π}{2}}\left\{\displaystyle\frac{5(1-\cos2θ)}{2}+3(\cos6θ-\cos4θ)+\displaystyle\frac{1-\cos10θ}{2}\right\}dθ\)
\(=5\left[3θ-\displaystyle\frac{5}{4}\sin2θ+\displaystyle\frac{1}{2}\sin6θ-\displaystyle\frac{3}{4}\sin4θ-\displaystyle\frac{1}{20}\sin10θ\right]_{0}^{\frac{π}{2}}\)
(\(\sin\)の部分は全部\(0\))
\(=\displaystyle\frac{15}{2}π\)
(例題2)
\(xy\)平面において、原点\(O\)を中心とする半径\(4\)の円\(C\)の内側を半径\(1\)の円\(C’\)が内接しながら滑ることなく転がるとき、円\(C’\)上の点\(P\)が描く曲線を\(X\)とする。ただし、点\(P\)のはじめの位置は点\(P_0(4,0)\)とする。円\(C’\)の中心\(O’\)が原点\(O\)のまわりを\(θ\)だけ回転したときの点\(P\)の座標を\((x,y)\)とするとき、「\(x,y\)を\(θ\)を用いて表せ」。
(例題1)と同様に、等しい長さの円弧に着目してベクトルを用いて求めます。
ちなみにハイポサイクロイド(内サイクロイド)で半径の比が 4:1 なので軌跡はアステロイドになります。
(解答)
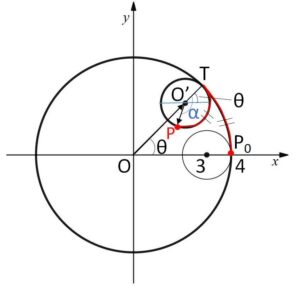
\(\stackrel{\huge\frown}{TP}=\stackrel{\huge\frown}{P_0T}\) だから
\(4θ=1α\)
よって \(α=4θ\)
よって
\(\overrightarrow{O’P}=(\cos(θ-α),\sin(θ-α))\)
\(=(\cos(-3θ),\sin(-3θ))\)
\(=(\cos3θ,-\sin3θ)\)
ゆえに \(OO’=4-1=3\) だから
\(\overrightarrow{OP}=\overrightarrow{OO’}+\overrightarrow{O’P}\)
\(=(3\cosθ,3\sinθ)+(\cos3θ,-\sin3θ)\)
\(=(3\cosθ+\cos3θ,3\sinθ-\sin3θ)\)
したがって\(P(x,y)\)の座標は
\(x=3\cosθ+\cos3θ\)
\(y=3\sinθ-\sin3θ\)
※3倍角の公式を使ってもう少し変形すると
\(x=4\cos^3θ\)
\(y=4\sin^3θ\)
となる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円と曲線と面積 back→媒介変数と面積②(トロコイド・サイクロイド)