面積と極限の例題です。
(例題1)
自然数\(n\)に対し、関数 \(f_n(x)=(n+1)x(1-x)^n\) が区間 \([0,1]\) で定義されている。この区間において、曲線 \(y=f_n(x)\) と\(x\)軸とで囲まれた図形の面積を\(S_n\)とする。
(1)\(S_n\)を求めよ。
(2)\(\displaystyle\lim_{n \to \infty}S_n\) を求めよ。
なお、\(n\)の奇偶で \(x>1\) の \(f_n(x)\) の正負は変わります。
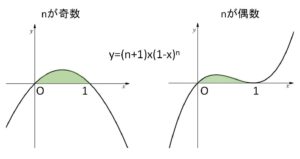
(1)
\(0≦x≦1\) において
\(f_n(x)=(n+1)x(1-x)^n≧0\) だから
\(S_n=(n+1)\displaystyle\int_{0}^{1}x(1-x)^ndx\)
\(=(n+1)\left[x\cdot\displaystyle\frac{-1}{n+1}(1-x)^{n+1}\right]_{0}^{1}+\displaystyle\int_{0}^{1}(1-x)^{n+1}dx\)
\(=\displaystyle\int_{0}^{1}(1-x)^{n+1}dx\)
\(=\left[\displaystyle\frac{-1}{n+2}(1-x)^{n+2}\right]_{0}^{1}\)
\(=\displaystyle\frac{1}{n+2}\)
(2)
\(\displaystyle\lim_{n \to \infty}S_n=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n+2}\)
\(=0\)
(例題2)
\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{nπ}e^{-x}|\sin x|dx\) を求めよ。
\(y=e^{-x}\sin x\) は徐々に振幅が小さくなる振動する曲線なので減衰曲線と呼ばれます。\(y=e^{-x}|\sin x|\) の積分は連なった山型の面積の和を求めることになりますが、\(π\)ごとに\(\sin x\)の正負が変わるので、分割して求めることになります。
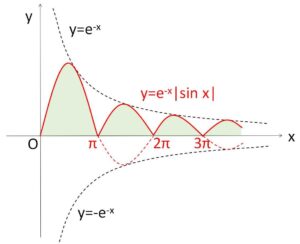
\(I=\displaystyle\int_{0}^{nπ}e^{-x}|\sin x|dx\) とおくと
\(I=\displaystyle\int_{0}^{π}e^{-x}|\sin x|dx+\displaystyle\int_{π}^{2π}e^{-x}|\sin x|dx+\cdots+\displaystyle\int_{(n-1)π}^{nπ}e^{-x}|\sin x|dx\)
\(=\displaystyle\sum_{k=1}^{n}\displaystyle\int_{(k-1)π}^{kπ}e^{-x}|\sin x|dx\)
(積分区間を \(0\)から\(π\) にするために置換積分。\(t=x-(k-1)π\) で置換する。または\(k\)の偶奇で場合分けしてもよい)
\(=\displaystyle\sum_{k=1}^{n}\displaystyle\int_{0}^{π}e^{-t-(k-1)π}|\sin\{t+(k-1)π\}|dt\)
\(=\displaystyle\sum_{k=1}^{n}e^{-(k-1)π}\displaystyle\int_{0}^{π}e^{-t}|(-1)^{k-1}\sin t|dt\)
\(=\displaystyle\sum_{k=1}^{n}(e^{-π})^{k-1}\displaystyle\int_{0}^{π}e^{-t}|\sin t|dt\)
\(=\displaystyle\sum_{k=1}^{n}(e^{-π})^{k-1}\displaystyle\int_{0}^{π}e^{-t}\sin tdt\)
(定積分を求めます)
ここで
\((e^{-t}\sin t)’=-e^{-t}\sin t+e^{-t}\cos t\)
\((e^{-t}\cos t)’=-e^{-t}\sin t-e^{-t}\cos t\)
より
\(\displaystyle\int_{0}^{π}e^{-t}\sin t=\left[-\displaystyle\frac{1}{2}(e^{-t}\sin t+e^{-t}\cos t)\right]_{0}^{π}\)
\(=\displaystyle\frac{e^{-π}+1}{2}\)
よって
\(\displaystyle\lim_{n \to \infty}\displaystyle\int_{0}^{nπ}e^{-x}|\sin x|dx\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{n}(e^{-π})^{k-1}\cdot\displaystyle\frac{e^{-π}+1}{2}\)
\(=\displaystyle\frac{e^{-π}+1}{2}\displaystyle\sum_{k=1}^{\infty}(e^{-π})^{k-1}\)
(公比\(e^{-π}\)の無限等比級数だから収束して)
\(=\displaystyle\frac{e^{-π}+1}{2}\cdot\displaystyle\frac{1}{1-e^{-π}}\)
(分母分子 \(e^{π}\) 倍して)
\(=\displaystyle\frac{e^{π}+1}{2(e^{π}-1)}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→逆関数と面積 back→円と曲線と面積