2曲線線で囲まれる面積についてです。
・2曲線で囲まれる面積
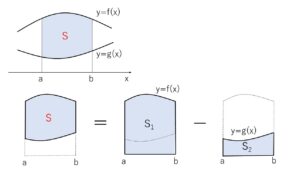
2曲線 \(y=f(x)\)、\(y=g(x)\) と \(x=a\)、\(x=b\) (\(a<b\)) で囲まれる部分の面積\(S\)は次のように定積分で求めることができます。
\(S=\displaystyle\int_{a}^{b}|f(x)-g(x)|dx\)
詳しくは →定積分と面積の関係 を参照して下さい。
\(x\)軸とではさまれる部分の面積と同様に被積分関数に絶対値がつきますが、実際に計算する場合には\(f(x),g(x)\)の大小で場合分けして分割することになります。\(f(x),g(x)\)の大小関係だけに気を付ければよく、グラフがどの位置にあるかは問いません。(\(y<0\) の部分にあってもよい)
大小関係は差をとり(交点の\(x\)座標も分かる)、必要ならば微分することで把握します。
もしくはグラフの概形から判断します。
(例題1)
2曲線 \(y=\sin x\)、\(y=\cos x\) (いずれも \(0≦x≦\displaystyle\frac{3}{2}π\)) で囲まれる図形の面積を求めよ。
(解答)
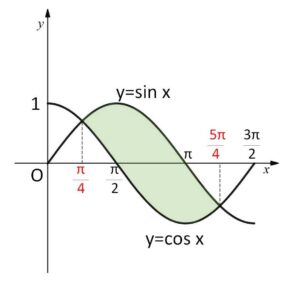
\(\sin x-\cos x=0\) を解くと
\(\sqrt{2}\sin(x-\displaystyle\frac{π}{4})=0\)
\(0≦x≦\displaystyle\frac{3}{2}π\) より
\(x-\displaystyle\frac{π}{4}=0,π\)
よって交点の\(x\)座標は
\(x=\displaystyle\frac{π}{4}、\displaystyle\frac{5}{4}π\)
よって面積は
\(\displaystyle\int_{\frac{π}{4}}^{\frac{5}{4}π}(\sin x-\cos x)dx\)
\(=[-\cos x-\sin x]_{\frac{π}{4}}^{\frac{5}{4}π}\)
\(=(\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{2}})+(\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{2}})\)
\(=2\sqrt{2}\)
(例題2)
(1)\(0≦x≦2π\) において、関数 \(f(x)=\displaystyle\frac{e^x}{\cos x}\) の増減を調べ、極値を求めよ。
(2)\(k\)を定数とするとき、\(x\)についての方程式 \(e^{x}=k\cos x\) の \(0≦x≦2π\) における異なる実数解の個数を求めよ。
(3)\(0≦x≦2π\) の範囲で、2つの曲線 \(y=e^{x}\)、\(y=\sqrt{2}e^{\frac{π}{4}}\cos x\)、および2つの直線 \(x=0\)、\(x=2π\) とで囲まれた部分の面積を求めよ。
(解答)
(1)
\(f(x)=\displaystyle\frac{e^x}{\cos x}\)
\(x≠\displaystyle\frac{π}{2},\displaystyle\frac{3}{2}π\) であり
\(f'(x)=\displaystyle\frac{e^x\cos x-e^{x}(-\sin x)}{\cos^2x}\)
\(=\displaystyle\frac{\sqrt{2}e^x}{\cos^2x}\sin(x+\displaystyle\frac{π}{4})\)
\(\sin(x+\displaystyle\frac{π}{4})\) の符号を考えると、増減表は以下の通り。
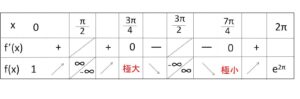
よって
極大値 \(f(\displaystyle\frac{3}{4}π)=-\sqrt{2}e^{\frac{3}{4}π}\)
極小値 \(f(\displaystyle\frac{7}{4}π)=\sqrt{2}e^{\frac{7}{4}π}\)
をとる。
(2)
\(e^{x}=k\cos x\) (\(0≦x≦2π\))
\(e^{x}>0\) より \(\cos x=0\) を満たす\(x\)はこの方程式の解にはならない。
よって \(\cos x≠0\) だから
\(k=\displaystyle\frac{e^x}{\cos x}\)
の解の個数を考えればよい。
(1)より \(y=f(x)=\displaystyle\frac{e^x}{\cos x}\) (\(0≦x≦2π\))
のグラフは以下のようになる。
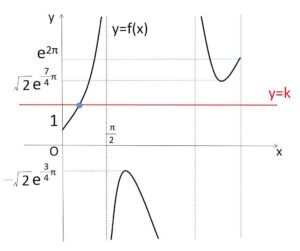
したがって異なる解の個数は、\(y=k\) と \(y=f(x)\) の共有点の個数を調べると
\(k>e^{2π}\) のとき 2個
\(\sqrt{2}e^{\frac{7}{4}π}<k≦e^{2π}\) 3個
\(k=\sqrt{2}e^{\frac{7}{4}π}\) のとき 2個
\(1≦k<\sqrt{2}e^{\frac{7}{4}π}\) のとき 1個
\(-\sqrt{2}e^{\frac{3}{4}π}<k<1\) のとき 0個
\(k=-\sqrt{2}e^{\frac{3}{4}π}\) のとき 1個
\(k<-\sqrt{2}e^{\frac{3}{4}π}\) のとき 2個
(3)
\(e^x=\sqrt{2}e^{\frac{π}{4}}\cos x\)・・・①
を解くことになりますが、まず(2)より \(k=\sqrt{2}e^{\frac{π}{4}}\) の場合に該当するので、交点は\(1\)個です。①は直接解くことはできませんが、色々値を代入すると1つの解が \(x=\displaystyle\frac{π}{4}\) であることは分かり、交点が1個なのでこれ以外に解はありません。(グラフより \(0<x<\displaystyle\frac{π}{2}\) の範囲に解があることは分かるので、この範囲で色々試してみる)
グラフの大小関係については、(2)のグラフからも考えることはできますが、2つの曲線はそこまで複雑ではないので、直接グラフを描いた方が楽です。
\(e^x=\sqrt{2}e^{\frac{π}{4}}\cos x\)・・・① (\(0≦x≦2π\))
方程式①は、(2)の \(k=\sqrt{2}e^{\frac{π}{4}}\) に該当し
\(\sqrt{2}e^{0}<\sqrt{2}e^{\frac{π}{4}}\) だから
\(1<\sqrt{2}e^{\frac{π}{4}}<\sqrt{2}e^{\frac{7}{4}π}\)
よって①の実数解の個数は1個であり、①に \(x=\displaystyle\frac{π}{4}\) を代入すると成り立つので、これが解である。
ゆえに \(y=e^{x}\) と \(y=\sqrt{2}e^{\frac{π}{4}}\cos x\) のグラフの交点は \(0≦x≦2π\) の範囲では1つであり、交点の\(x\)座標は \(x=\displaystyle\frac{π}{4}\) だから、2曲線のグラフの概形は次の通り。
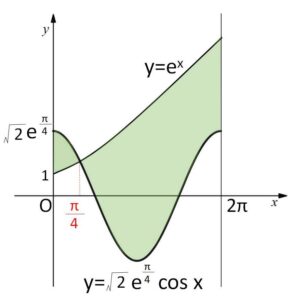
したがって求める面積\(S\)は
\(S=\displaystyle\int_{0}^{\frac{π}{4}}(\sqrt{2}e^{\frac{π}{4}}\cos x-e^{x})dx+\displaystyle\int_{\frac{π}{4}}^{2π}(e^x-\sqrt{2}e^{\frac{π}{4}}\cos x)dx\)
\(=[\sqrt{2}e^{\frac{π}{4}}\sin x-e^{x}]_{0}^{\frac{π}{4}}+[e^x-\sqrt{2}e^{\frac{π}{4}}\sin x]_{\frac{π}{4}}^{2π}\)
\(=(e^{\frac{π}{4}}-e^{\frac{π}{4}}+1)+(e^{2π}-e^{\frac{π}{4}}+e^{\frac{π}{4}})\)
\(=1+e^{2π}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2曲線で囲まれる面積②(交点が具体的にでない) back→定積分と面積