接線や接する2曲線に関する面積の例題です。
(例題1)
曲線 \(C_1:y=e^x\) と 曲線 \(C_2:y=a\sqrt{x}\) がある。
(1)\(C_1\)と\(C_2\)が共有点で共通の接線をもつとき、\(a\)の値を定め、接線の方程式を求めよ。
(2)\(a\)の値が(1)で定まるとき、\(C_1,C_2\)と\(y\)軸で囲まれる図形の面積を求めよ。
①\(f(t)=g(t)\) ②\(f'(t)=g'(t)\)
が成り立つことを利用します。素直に接線が一致するとして接線の方程式をそれぞれ出して
①\(y\)切片が等しい ②接線の傾きが等しい
としてもよいです。意味としては同じ式が出てきます。
(解答)
(1)
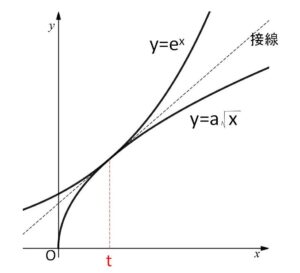
接点の\(x\)座標を\(t\)とおくと、2曲線が共通の接線をもつので
\((a\sqrt{x})’=\displaystyle\frac{a}{2\sqrt{x}}\) より
\(e^t=a\sqrt{t}\)・・・①
\(e^{t}=\displaystyle\frac{a}{2\sqrt{t}}\)・・・②
①②より
\(a\sqrt{t}=\displaystyle\frac{a}{2\sqrt{t}}\)
\(e^{t}>0\) だから①より \(a≠0\) となるので
\(t=\displaystyle\frac{1}{2}\)
よって①より
\(a=\sqrt{2e}\)
接線の方程式は
\(y=e^{t}(x-t)+e^t\)
だから (\(y=a\sqrt{x}\) のほうでやっても同じ)
\(y=\sqrt{e}(x-\displaystyle\frac{1}{2})+\sqrt{e}\)
(2)
面積は積分するだけです。
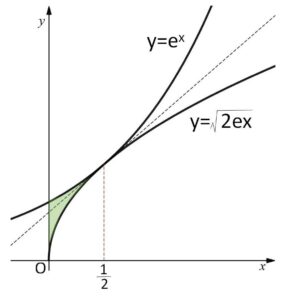
面積\(S\)は
\(S=\displaystyle\int_{0}^{\frac{1}{2}}(e^x-\sqrt{2e}\sqrt{x})dx\)
\(=\left[e^x-\sqrt{2e}\cdot\displaystyle\frac{2}{3}x^{\frac{3}{2}}\right]_{0}^{\frac{1}{2}}\)
\(=\sqrt{e}-\displaystyle\frac{2\sqrt{2e}}{3}\cdot\displaystyle\frac{1}{2\sqrt{2}}-1\)
\(=\displaystyle\frac{2\sqrt{e}}{3}-1\)
(例題2)
\(xy\)平面上の曲線 \(y=\displaystyle\frac{1}{x}\) (\(x>0\)) を\(C\)とする。
(1)点 \((a,\displaystyle\frac{3}{4a})\) (\(a>0\)) から曲線\(C\)に引いた2本の接線の方程式を求めよ。
(2) (1)で求めた2本の接線と曲線\(C\)で囲まれた図形の面積を求めよ。
なお、\((a,\displaystyle\frac{3}{4a})\) は、\(a>0\) より \(y=\displaystyle\frac{1}{x}\) (\((a,\displaystyle\frac{1}{a})\) が曲線上にある) の下側にあります。
(解答)
(1)
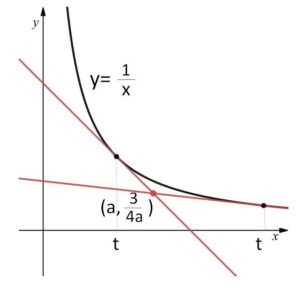
接点の\(x\)座標を\(t\ (>0)\)とおくと、接線の方程式は \((\displaystyle\frac{1}{x})’=-\displaystyle\frac{1}{x^2}\) より
\(y=-\displaystyle\frac{1}{t^2}(x-t)+\displaystyle\frac{1}{t}\)
よって
\(y=-\displaystyle\frac{1}{t^2}x+\displaystyle\frac{2}{t}\)・・・①
接線は (\(a,\displaystyle\frac{3}{4a}\)) を通るから
\(\displaystyle\frac{3}{4a}=-\displaystyle\frac{1}{t^2}a+\displaystyle\frac{2}{t}\)
両辺\(4at^2\)倍して整理すると
\(3t^2-8at+4a^2=0\)
\((3t-2a)(t-2a)=0\)
\(t=\displaystyle\frac{2a}{3},2a\)
したがって2本の接線の方程式は①より
\(y=-\displaystyle\frac{9}{4a^2}x+\displaystyle\frac{3}{a}\)
\(y=-\displaystyle\frac{1}{4a^2}x+\displaystyle\frac{1}{a}\)
(2)
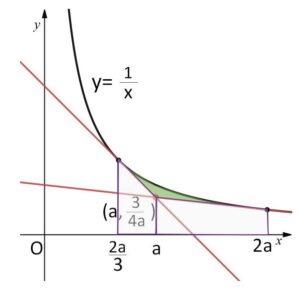
求める面積\(S\)は、\(y=\displaystyle\frac{1}{x}\) と\(x\)軸との間の図形から、台形2つを除いた図形の面積だから
\(S=\displaystyle\int_{\frac{2}{3}a}^{2a}\displaystyle\frac{1}{x}dx-\displaystyle\frac{1}{2}(\displaystyle\frac{3}{2a}+\displaystyle\frac{3}{4a})\cdot\displaystyle\frac{a}{3}-\displaystyle\frac{1}{2}(\displaystyle\frac{3}{4a}+\displaystyle\frac{1}{2a})\cdot a\)
\(=\log2a-\log\displaystyle\frac{2}{3}a-\displaystyle\frac{3}{8}-\displaystyle\frac{5}{8}\)
\(=\log\displaystyle\frac{2a}{\displaystyle\frac{2}{3}a}-1\)
\(=\log3-1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→面積の最大・最小 back→y軸方向の積分と面積