陰関数と面積

陰関数と面積についてです。

・楕円の面積
陰関数で表される曲線で囲まれる面積は

\(y=(xの式)\) または \(x=(yの式)\)

として定積分を計算するのが基本となります。その際、定義域には注意します。
また、図形の対称性に着目して計算を楽にするという工夫も重要です。

例として楕円の面積計算を挙げてみます。

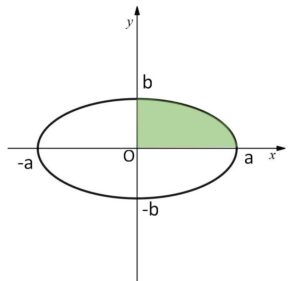
楕円 \(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\)・・・①  (\(a,b\)は正の数) で囲まれた図形の面積\(S\)は、①が\(x,y\)軸について対称であることから、第1象限での面積を考えて\(4\)倍すればよい。

①より \(y≧0\) のとき
\(y=\sqrt{b^2-\displaystyle\frac{b^2}{a^2}x^2}\)
\(=\displaystyle\frac{b}{a}\sqrt{a^2-x^2}\)
となるから

\(S=4\cdot\displaystyle\frac{b}{a}\displaystyle\int_{0}^{a}\sqrt{a^2-x^2}dx\)

(半径\(a\)の円の\(\frac{1}{4}\)。\(x=a\sinθ\) で置換してもよい)

\(=4\cdot\displaystyle\frac{b}{a}\cdot\displaystyle\frac{1}{4}πa^2\)

\(=πab\)

もしくは、次のように拡大縮小を考えて円の面積に帰着させる方法もあります。

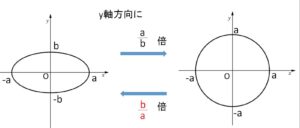
楕円上の各点を\(y\)軸方向に\(\displaystyle\frac{a}{b}\)倍すると、半径\(a\)の円になり、その面積は\(πa^2\)。\(y\)軸方向に \(\displaystyle\frac{b}{a}\)倍すると元の楕円に戻るので、楕円の面積\(S\)は
\(S=πa^2\cdot\displaystyle\frac{b}{a}=πab\)

※曲線上の点を\(y\)軸方向にのみ\(k\)倍すると、面積も\(k\)倍になるという事実を用いています。これは\(ky\)の定積分が
\(\displaystyle\int_{α}^{β} kydx=k\displaystyle\int_{α}^{β} ydx\)
となることから分かります。(感覚的には縦方向だけ\(k\)倍するので、面積も\(k\)倍になる)

また 楕円 \(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\)・・・① 上の各点を\(y\)軸方向に\(\displaystyle\frac{a}{b}\)倍すると円になるのは、移動後の点を\((X,Y)\)とすると

\(X=x\)、\(Y=\displaystyle\frac{a}{b}y\)
つまり
\(x=X\)、\(y=\displaystyle\frac{b}{a}Y\)
であり、これらを①に代入すると
\(\displaystyle\frac{X^2}{a^2}+\displaystyle\frac{Y^2}{a^2}=1\)

\(X^2+Y^2=a^2\)
となることから分かります。

(例題)
(1)曲線 \(\sqrt[3]{x}+\sqrt[3]{y}=1\) (\(x≧0\)、\(y≧0\)) と \(x\)軸、\(y\)軸で囲まれた図形の面積を求めよ。

(2)曲線 \(2x^2-2xy+y^2-4x+3=0\) で囲まれた図形の面積を求めよ。

(解答)
(1)
\(\sqrt[3]{x}+\sqrt[3]{y}=1\) (\(x≧0\)、\(y≧0\)) より

\(\sqrt[3]{y}=1-\sqrt[3]{x}\)・・・①
\(y≧0\) だから \(1-\sqrt[3]{x}≧0\)
よって、\(x≧0\) と合わせると
\(0≦x≦1\)

①の両辺を3乗して
\(y=(1-\sqrt[3]{x})^3\)　(単調減少)
\(y=1-3\sqrt[3]{x}+3\sqrt[3]{x^2}-x\)

(\(y≧0\) なのでこのまま積分してよい。微分するとグラフの概形が正確に分かる)

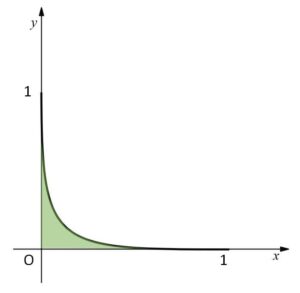
よって面積\(S\)は
\(S=\displaystyle\int_{0}^{1}(1-3x^{\frac{1}{3}}+3x^{\frac{2}{3}}-x)dx\)

\(=\left[x-\displaystyle\frac{9}{4}x^{\frac{4}{3}}+\displaystyle\frac{9}{5}x^{\frac{5}{3}}-\displaystyle\frac{1}{2}x^2\right]_{0}^{1}\)

\(=1-\displaystyle\frac{9}{4}+\displaystyle\frac{9}{5}-\displaystyle\frac{1}{2}\)

\(=\displaystyle\frac{1}{20}\)

(2)
\(2x^2-2xy+y^2-4x+3=0\)

(\(y\)の2次方程式を解の公式を使って解く)

\(y\)について整理すると
\(y^2-2xy+2x^2-4x+3=0\)
よって
\(y=x±\sqrt{x^2-(2x^2-4x+3)}\)

\(y=x±\sqrt{-x^2+4x-3}\)

定義域は
\(-x^2+4x-3≧0\) より
\((x-1)(x-3)≦0\)
\(1≦x≦3\)

(グラフの概形を微分して調べます。微分しなくても判断できる方法もあります(後述)。)

\(y=x+\sqrt{-x^2+4x-3}\) について
\(y’=1+\displaystyle\frac{-2x+4}{2\sqrt{-x^2+4x-3}}\)

\(=\displaystyle\frac{\sqrt{-x^2+4x-3}+(-x+2)}{\sqrt{-x^2+4x-3}}\)

(ア) \(1<x<2\) のとき
\(-x+2>0\) だから \(y’>0\)

(イ)\(2≦x<3\) のとき
\(-x+2≦0\) で、２乗して絶対値を比較すると
\(-x^2+4x-3>(-x+2)^2\) を満たすのは
\(2x^2-8x+7<0\)
\(\displaystyle\frac{4-\sqrt{2}}{2}<x<\displaystyle\frac{4+\sqrt{2}}{2}\ (=2+\displaystyle\frac{1}{\sqrt{2}})\)

よって
\(2≦x<2+\displaystyle\frac{1}{\sqrt{2}}\) のとき \(y’>0\)
\(2+\displaystyle\frac{1}{\sqrt{2}}<x<3\) のとき \(y'<0\)

\(y=x-\sqrt{-x^2+4x-3}\) も同様に検討して、\(x=1,3\)で2つのグラフは交わることも合わせると曲線の概形は次のようになる。

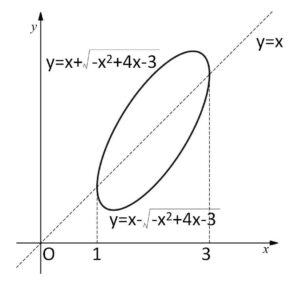
したがって曲線で囲まれる図形の面積\(S\)は

\(S=\displaystyle\int_{1}^{3}\{x+\sqrt{-x^2+4x-3}-(x-\sqrt{-x^2+4x-3})\}dx\)

\(=2\displaystyle\int_{1}^{3}\sqrt{-x^2+4x-3}\ dx\)

(\(y=\sqrt{-x^2+4x-3}\) とおいて2乗すると円になることが分かります。)

\(=2\displaystyle\int_{1}^{3}\sqrt{1-(x-2)^2}\ dx\)

(積分は半径\(1\)の半円の面積)

\(=2\cdot\displaystyle\frac{1}{2}\cdot1^2π\)

\(=π\)

※グラフの概形を微分せずに掴む方法
\(y=x+\sqrt{-x^2+4x-3}\) と \(y=x-\sqrt{-x^2+4x-3}\) は\(x\)の部分が共通なので、これを基にして \(\sqrt{-x^2+4x-3}\) の分だけ 上乗せ または 除かれる と考えることができます。
\(y=±\sqrt{-x^2+4x-3}\) は2乗すると円の方程式であることが分かるので、この円の曲線の分だけ 上乗せ または 除かれる とすれば概形が分かります。この方法だと細かい増減は分かりませんが、2つのグラフの上下関係などは分かるので、面積を計算するだけなら十分です。

(参考)2次曲線
\(x,y\)の2次式で表される方程式が表す曲線は次のように分類されます。

①円　②楕円　③双曲線　④放物線
⑤直線 (1次式の積に因数分解できる場合)
⑥点 (\(x^2+y^2=0\) など)
⑦座標平面上に存在しない (\(x^2+y^2+4=0\) など)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→媒介変数と面積①　back→面積の最大・最小