体積と断面積の積分の関係について見ていきます。
こちらも参考にして下さい。→定積分と体積の関係
・断面積の積分と体積
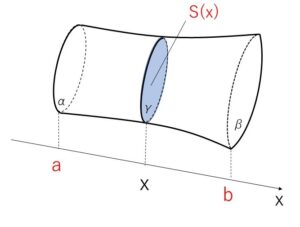
\(x\)軸に垂直な平面\(α,β\)があり、それぞれの平面と\(x\)軸との交点を\(a,b\)とする。
平面\(α,β\)にはさまれた立体の面積を\(V\)とし、\(x\)軸に垂直で\(x\)軸との交点の座標が\(x\)である平面\(γ\)による立体の断面積を\(S(x)\)とする。このとき\(V\)次のように定積分で表される。
\(V=\displaystyle\int_{a}^{b}S(x)dx\)
簡単に言ってしまうと、微小な体積 \(ΔV=S(x)Δx\) を積み上げるということですが、丁寧に証明すると次の通りです。
(証明)
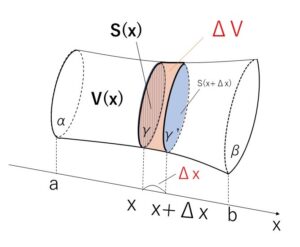
\(V(x)\)を、平面\(α\)と平面\(γ\)にはさまれた部分の立体の体積とする(\(a\)から\(x\)までの部分ということ)。
\(x\)から\(x+Δx\)までの\(S(x)\)の最大値と最小値をそれぞれ\(S_M,S_m\)とし、この間の微小体積を \(ΔV=V(x+Δx)-V(x)\) とすると、次の不等式が成り立つ。(最大面の柱型の体積と最小面の柱型の体積の間にある)
\(S_mΔx≦ΔV≦S_MΔx\)
\(Δx>0\) のとき
\(S_m≦\displaystyle\frac{ΔV}{Δx}≦S_M\)・・・①
\(Δx \to 0\) のとき \(S_m,S_M \to S(x)\) となるから、はさみうちの原理より
\(\displaystyle\frac{dV}{dx}=S(x)\)・・・②
(\(Δx<0\) のときも①の不等号が逆になるだけで②が成り立つ)
\(V(x)\)の定義から \(V(b)=V\)、\(V(a)=0\) となるので、全体の体積\(V\)は
\(V=V(b)\)
\(=V(b)-V(a)\)
\(=[V(x)]_{a}^{b}\)
\(=\displaystyle\int_{a}^{b}V'(x)dx\)
\(=\displaystyle\int_{a}^{b}S(x)dx\)
(例題)
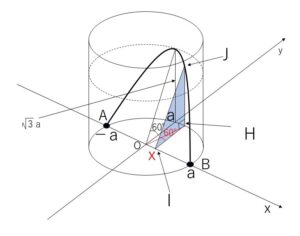
底面の半径が\(a\)、高さが\(2a\)の直円柱がある。この底面の直径\(AB\)を含み、底面と\(60°\)の傾きをなす平面で、直円柱を2つの部分に分ける。この2つの部分のうち、小さいほうの立体の体積を求めよ。
積分する軸を選んだ後は、その変数のとりうる範囲(積分区間になる)には注意します。
(解答1)\(x\)軸に垂直に切る
これらのことは式で表現するとより分かりやすくなります(参考参照)。
なお、本問では\(60°\)平面が円柱の上面と交わらないので断面はどこも三角形になりますが、上面と交わる(1点で交わる場合を除く)ときは台形になる部分もでてきます。

図のように座標軸を設定し、\(x\)軸に垂直な断面を考える。
図より \(IH=\sqrt{a^2-x^2}\)
\(HJ=IH\tan60°=\sqrt{3}\sqrt{a^2-x^2}\) だから、\(-a≦x≦a\) のとき \(x\)座標が\(x\)である断面を\(S(x)\)とすると、断面は直角三角形だから
\(S(x)=\displaystyle\frac{\sqrt{3}}{2}(a^2-x^2)\)
したがって求める体積\(V\)は
\(V=\displaystyle\int_{-a}^{a}\displaystyle\frac{\sqrt{3}}{2}(a^2-x^2)dx\)
\(=\sqrt{3}\displaystyle\int_{0}^{a}(a^2-x^2)dx\)
\(=\sqrt{3}\left[a^2x-\displaystyle\frac{1}{3}x^3\right]_{0}^{a}\)
\(=\displaystyle\frac{2\sqrt{3}}{3}a^3\)
(参考)式で断面を捉える
円柱の側面および内部の方程式は
\(x^2+y^2≦a^2\)・・・① (\(0≦z≦2a\)・・・②)
\(60°\)をなす平面の方程式の下側は
\(z≦\sqrt{3}y\)・・・③ (\(x\)は任意)
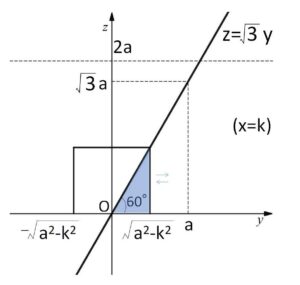
分かりやすくするために、\(x=k\) (\(-a≦k≦a\)) と固定すると①より
\(-\sqrt{a^2-k^2}≦y≦\sqrt{a^2-k^2}\)・・・①’
①’②③の共通部分を\(yz\)平面に図示すると次のように断面が直角三角形になる。(\(k\)の値によらない)
数式で表すと立体をイメージすることなく処理ができるところが良いところです。
以下\(y,z\)軸に垂直な断面の場合も式で捉えることができますが、省略します。
(解答2)\(y\)軸に垂直に切る
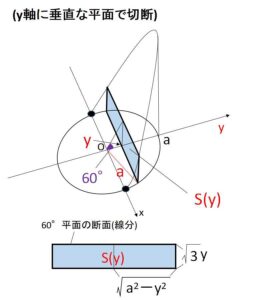
\(y\)軸に垂直な断面を考える。\(0≦y≦a\) として \(y\)座標が\(y\)である断面を\(S(y)\)とすると、断面は長方形になるので
\(S(y)=2\sqrt{a^2-y^2}\cdot(\tan60°)y\)
よって体積\(V\)は
\(V=2\sqrt{3}\displaystyle\int_{0}^{a}y\sqrt{a^2-y^2}dy\)
\(=2\sqrt{3}\left[(-\displaystyle\frac{1}{2})\cdot\displaystyle\frac{2}{3}(a^2-y^2)^{\frac{3}{2}}\right]_{0}^{a}\)
\(=2\sqrt{3}\cdot\displaystyle\frac{1}{2}\cdot\displaystyle\frac{2}{3}\cdot a^3\)
\(=\displaystyle\frac{2\sqrt{3}}{3}a^3\)
(解法3)\(z\)軸に垂直に切る
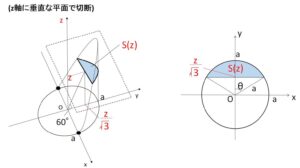
\(z\)軸に垂直に切る。\(0≦z≦\sqrt{3}a\) とし、断面の\(z\)座標が\(z\)であるときの断面を\(S(z)\)とおく。上右図のように\(θ\) (\(0≦θ≦\displaystyle\frac{π}{2}\)) を設定すると
\(S(z)=2(\displaystyle\frac{1}{2}a^2θ-\displaystyle\frac{1}{2}a\cdot a\cosθ\sinθ)\)
\(=a^2(θ-\sinθ\cosθ)\)
\(a\cosθ=\displaystyle\frac{z}{\sqrt{3}}\) の関係式より
\(-a\sinθ=\displaystyle\frac{dz}{\sqrt{3}}\)
となるから、体積\(V\)は
\(V=\displaystyle\int_{0}^{\sqrt{3}a}S(z)dz\)
\(=\displaystyle\int_{\frac{π}{2}}^{0}a^2(θ-\sinθ\cosθ)(-\sqrt{3}a\sinθ)dθ\)
\(=\sqrt{3}a^3\displaystyle\int_{0}^{\frac{π}{2}}(θ\sinθ-\sin^2θ\cosθ)dθ\)
(前半は部分積分)
\(=\sqrt{3}a^3\left[-θ\cosθ+\sinθ-\displaystyle\frac{1}{3}\sin^3θ\right]_{0}^{\frac{π}{2}}\)
\(=\displaystyle\frac{2\sqrt{3}}{3}a^3\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→回転体の体積 back→極座標と面積