空間において線分を回転させてできる立体の体積を求める問題です。
(例題)
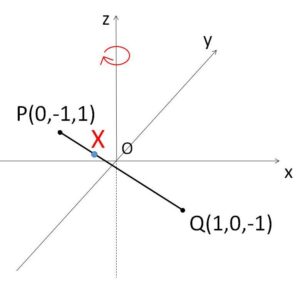
\(xyz\)空間内に2点 \(P(0,-1,1)\) と \(Q(1,0,-1)\) がある。線分\(PQ\) (端点を含む) を\(z\)軸周りに1回転してできる曲面と2つの平面 \(z=1\),\(z=-1\) で囲まれた立体を\(A\)とする。
(1)\(t\)は実数とする。立体\(A\)を平面 \(z=t\) で切ったときの断面の面積\(S(t)\)を求めよ。
(2)立体\(A\)の体積を求めよ。
なお線分の端点の\(z\)座標が\(1,-1\)だから、\(z>1,z<-1\) の領域には立体は存在しないので、これも明記しておきます。
(解答)
(1)
\(t<-1,t>1\) のとき \(S(t)=0\)
\(-1≦t≦1\) のとき
線分\(PQ\)上にある点を\(X\)とおく。\(0≦k≦1\) とすると
\(\overrightarrow{OX}=\overrightarrow{OP}+k\overrightarrow{PQ}\)
\(=(0,-1,1)+k(1,1,-2)\)
\(=(k,-1+k,1-2k)\)
(\(z=t\) として\(k\)を決定します)
\(X\)が 平面 \(z=t\) と線分\(PQ\)の交点のとき
\(t=1-2k\) より
\(k=\displaystyle\frac{1-t}{2}\)
よってこのとき
\(\overrightarrow{OX}=(\displaystyle\frac{1-t}{2},-\displaystyle\frac{1+t}{2},t)\)
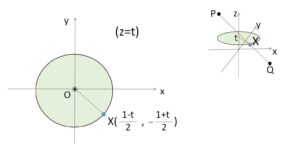
したがって \(z=t\) における断面は、半径\(\sqrt{(\displaystyle\frac{1-t}{2})^2+(-\displaystyle\frac{1+t}{2})^2}\) の円になるから
\(S(t)=π\left\{(\displaystyle\frac{1-t}{2})^2+(-\displaystyle\frac{1+t}{2})^2\right\}\)
\(=\displaystyle\frac{1+t^2}{2}π\)
答
\(t<-1,t>1\) のとき \(S(t)=0\)
\(-1≦t≦1\) のとき \(S(t)=\displaystyle\frac{1+t^2}{2}π\)
(参考)内分点の公式を利用する場合
\(X\)は直線上の点になるので内分点の公式を利用すると簡単に座標を求めることが可能です。
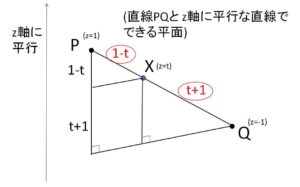
\(P(0,-1,1),\ Q(1,0,-1),\ X\)の\(z\)座標に着目すると、\(X\)の\(z\)座標が\(t\)のとき、\(PQ\)を \(1-t:t+1\) に内分しています。この内分比でそのまま線分\(PQ\)も内分しているので、\(x,y\)座標もこの比で内分されていることになります。よって\(X\)の\(x,y\)座標は
\(x\)座標:\(\displaystyle\frac{(t+1)\cdot0+(1-t)\cdot1}{2}=\displaystyle\frac{1-t}{2}\)
\(y\)座標:\(\displaystyle\frac{(t+1)\cdot(-1)+(1-t)\cdot0}{2}=-\displaystyle\frac{1+t}{2}\)
(2)
(積分するだけです)
(1)より体積\(V\)は
\(V=\displaystyle\int_{-1}^{1}\displaystyle\frac{1+t^2}{2}πdt\)
(偶関数の積分)
\(=π\displaystyle\int_{0}^{1}(1+t^2)dt\)
\(=π\left[t+\displaystyle\frac{t^3}{3}\right]_{0}^{1}\)
\(=\displaystyle\frac{4}{3}π\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間の回転②(平面図形の回転) back→連立不等式と体積