空間の回転③(立体図形の回転)

立体図形を回転させてできる回転体の体積を求める問題です。

今回は回転前の断面が平面図形になりますが、やることは変わりません。回転前の断面図を考えて、軸から一番近い点と遠い点を探すだけです。

(例題1)
\(xyz\)空間において \(O(0,0,0)\)、\(A(1,1,0)\)、\(B(1,0,0)\)、\(C(1,0,2)\) を4頂点とする四面体\(OABC\)を\(z\)軸まわりに回転させてできる回転体を\(U\)とする。

(1)\(U\)を平面\(z=t\) (\(0≦t≦2\)) で切断したときの断面の面積\(S(t)\)を求めよ。
(2)\(U\)の体積を求めよ。

(解答)
(1)

回転前の断面は三角形になります。頂点は\(OC,AC,BC\) 上にありますが、これらの位置(座標)はベクトルや内分点の公式や相似比などを利用して求めます。
断面図が分かったら軸(\(z=t\) 上の\(xy\)平面では原点)から一番近い点と遠い点を探しますが、ポイントは垂線です。

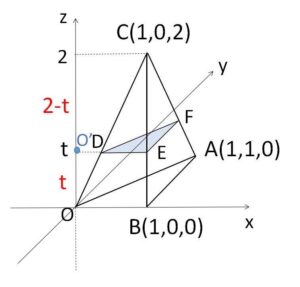
立体の回転例題1-1

平面\(z=t\) による四面体の断面は\(△DEF\)である。
\(D,E,F\)は線分\(OC,BC,AC\)をそれぞれ \(t:2-t\) に内分する点だから、\(D,E,F\)の座標は
\(D(\displaystyle\frac{t}{2},0,\displaystyle\frac{2t}{2})=(\displaystyle\frac{t}{2},0,t)\)
\(E(\displaystyle\frac{2-t+t}{2},0,\displaystyle\frac{2t}{2})=(1,0,t)\)
\(F(\displaystyle\frac{2-t+t}{2},\displaystyle\frac{2-t}{2},\displaystyle\frac{2t}{2})=(1,1-\displaystyle\frac{t}{2},t)\)

よって \(z=t\) 上で\(△DEF\)を図示すると次のようになる。

立体の回転例題1-2

一番近い点は\(D\)、遠い点は\(F\)です。この2点が描く円の間の領域を\(△DEF\)が埋めるように動くので(実際は線分\(DF\)だけで十分で残りは重複するだけ)、回転体の断面は2円の間の領域になります。

したがって、回転体の断面積は \(O'(0,0,t)\) とすると
\(S(t)=πO’F^2-πO’D^2\)
\(=π\{1^2+(1-\displaystyle\frac{t}{2})^2\}-π(\displaystyle\frac{t}{2})^2\)

\(=π(2-t)\)

(2)
(積分するだけです)
(1)より体積\(V\)は
\(V=\displaystyle\int_{0}^{2}π(2-t)dt\)

\(=π\left[2t-\displaystyle\frac{t^2}{2}\right]_{0}^{2}\)

\(=2π\)

(例題2)
\(xyz\)空間内の平面 \(z=0\) の上に正方形
\(R=\{(x,y,0)|1≦x≦2,\ 1≦y≦2\}\)
がある。正方形\(R\)を\(x\)軸のまわりに1回転してできる立体を\(K\)とする。\(K\)を\(y\)軸のまわりに1回転してできる立体\(L\)の体積を求めよ。

立体\(K\)は中をくり抜かれた円柱になり、この立体を回転させてできる立体の体積を求めることになります。回転前の立体\(K\)の断面を考えて回転させて、回転体\(L\)の断面積を求めて積分という流れになります。解答では数式で処理することにしますが、図と照らし合わせると、立体\(K\)を \(y=t\) で切断する際に真ん中の空洞を通る場合と通らない場合があり、場合分けが必要であることが分かります。

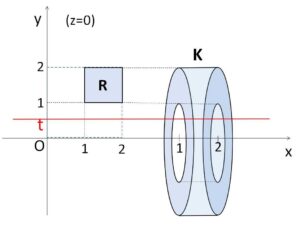
立体の回転例題2-1

正方形\(R\)を回転させてできる立体\(K\)は、内部をくり抜かれた円柱である。
立体\(K\)を表す方程式は
\(1≦y^2+z^2≦4\) かつ \(1≦x≦2\)・・・①

立体\(K\)は \(-2≦y≦2\) に存在し、\(xz\)平面について対称なので
\(0≦y≦2\) の範囲で考えればよい。

立体\(K\)を \(y=t\) (\(0≦t≦2\)) で切断したときの断面を表す方程式は①より
\(1≦t^2+z^2≦4\) かつ \(1≦x≦2\)
よって
\(1-t^2≦z^2≦4-t^2\) かつ \(1≦x≦2\)・・・②

(1つ目の不等式の左辺は \(t>1\) では平方根がとれないので場合分けします)
(i)\(0≦t≦1\) のとき
②は
\(z^2≧1-t^2\) かつ \(z^2≦4-t^2\) かつ \(1≦x≦2\)
であり、\(1-t^2<4-t^2\) より
\(-\sqrt{4-t^2}≦z≦-\sqrt{1-t^2}\) または \(\sqrt{1-t^2}≦z≦\sqrt{4-t^2}\)
かつ \(1≦x≦2\)・・・③
③を図示すると次の通り。

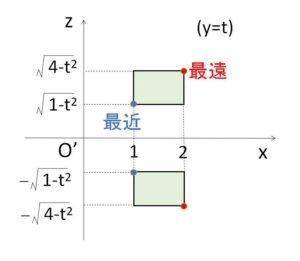
立体の回転例題2-2

回転軸上の点 \(O'(0,t,0)\) から最も近い点と遠い点を考えると、\(K\)の回転体\(L\)の断面積\(S(t)\)は
\(S(t)=π(2^2+4-t^2)-π(1^2+1-t^2)\)
\(=6π\)

(ii)\(1≦t≦2\) のとき
\(1-t^2≦0\) より \(1-t^2≦z^2\) は常に成り立つから②は
\(z^2≦4-t^2\) かつ \(1≦x≦2\)
よって
\(-\sqrt{4-t^2}≦z≦\sqrt{4-t^2}\) かつ \(1≦x≦2\)・・・④
④を図示すると次の通り。

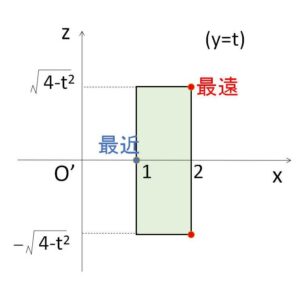
立体の回転例題2-3

同様に\(O'(0,t,0)\) から最も近い点と遠い点を考えると
\(S(t)=π(2^2+4-t^2)-π\cdot1^2\)
\(=π(7-t^2)\)

したがって回転体\(L\)の体積\(V\)は
\(V=2\left\{\displaystyle\int_{0}^{1}6πdt+\displaystyle\int_{1}^{2}π(7-t^2)dt\right\}\)

\(=12π\left[t\right]_{0}^{1}+2π\left[7t-\displaystyle\frac{1}{3}t^3\right]_{1}^{2}\)

\(=12π+2π(7-\displaystyle\frac{7}{3})\)

\(=\displaystyle\frac{64}{3}π\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→立体の共通部分　 back→空間の回転②(平面図形の回転)