斜め方向の直線に関する回転体の体積を求める例題です。
(例題1)
\(xy\)平面において、\(y=x^2\) と 直線 \(y=x\) によって囲まれた図形を直線 \(y=x\) の周りに回転させてできる回転体の体積を求めよ。
(i)斜め方向の座標\(t\)を設定して、\(t\)方向で積分する方法
(ii)全体を回転させて、回転軸を\(x,y\)軸に一致させる方法
(解答1)斜め方向に積分する方法
(ア)切断面の円の半径を素直に\(t\)で表して積分する方法
(イ)切断面の円の半径をもともとの変数\(x\)で表して置換積分する方法
があります。(イ)の方法でもスタートは\(t\)方向に積分する(最終的には\(x\)で積分する)ことに注意してください。
なお円の半径は点と直線の距離を使っても求まりますが、この例題だと\(45°\)の直角三角形が登場するので、辺の比を使ったほうが楽です。他の場面でもこの辺の比をフル活用します。
(ア)の方法
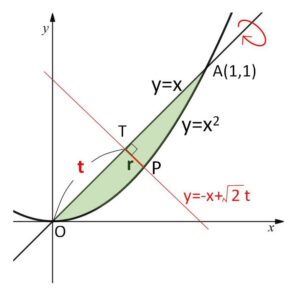
図の線分\(OA\ (=\sqrt{2})\) 上に点\(T\)をとる。
\(OT=t\) (\(0≦t≦\sqrt{2}\)) とおくと \(T(\displaystyle\frac{t}{\sqrt{2}},\displaystyle\frac{t}{\sqrt{2}})\)
\(T\)を通り、\(y=x\) に垂直な直線の方程式は
\(y=-(x-\displaystyle\frac{t}{\sqrt{2}})+\displaystyle\frac{t}{\sqrt{2}}\)
整理すると
\(y=-x+\sqrt{2}t\)・・・①
①と \(y=x^2\) の交点のうち、\(0≦x≦1\) の部分にあるほうを点\(P\)とおく。
\(x^2=-x+\sqrt{2}t\) を解くと
\(x^2+x-\sqrt{2}t=0\)
\(x=\displaystyle\frac{-1±\sqrt{1+4\sqrt{2}t}}{2}\)
小さい方の解は、負の値になるから点\(P\)の\(x\)座標は・・・(注)
\(x=\displaystyle\frac{-1+\sqrt{1+4\sqrt{2}t}}{2}\)
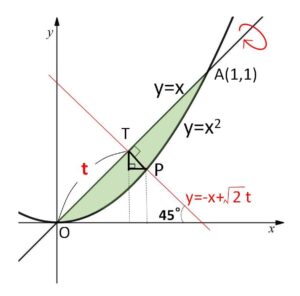
ここで\(45°\)の直角三角形の辺の比より
\(TP=\sqrt{2}\left|\displaystyle\frac{-1+\sqrt{1+4\sqrt{2}t}}{2}-\displaystyle\frac{t}{\sqrt{2}}\right|\)
\(=\left|\displaystyle\frac{-(1+\sqrt{2}t)+\sqrt{1+4\sqrt{2}t}}{\sqrt{2}}\right|\)
よって体積\(V\)は
\(V=\displaystyle\int_{0}^{\sqrt{2}}πTP^2dt\)
\(=\displaystyle\frac{π}{2}\displaystyle\int_{0}^{\sqrt{2}}\left\{-(1+\sqrt{2}t)+\sqrt{1+4\sqrt{2}t}\right\}^2dt\)
(1次式の根号は丸ごと置換が基本。\(u=\sqrt{1+4\sqrt{2}t}\) とすると
\(u^2=1+4\sqrt{2}t\))
\(=\displaystyle\frac{π}{2}\displaystyle\int_{1}^{3}\left\{-(1+\displaystyle\frac{u^2-1}{4})+u\right\}^2\cdot\displaystyle\frac{2u}{4\sqrt{2}}du\)
\(=\displaystyle\frac{π}{4^2\cdot4\sqrt{2}}\displaystyle\int_{1}^{3}(-u^2+4u-3)^2udu\)
\(=\displaystyle\frac{π}{4^3\sqrt{2}}\displaystyle\int_{1}^{3}(u^4+16u^2+9-8u^3-24u+6u^2)udu\)
\(=\displaystyle\frac{π}{4^3\sqrt{2}}\displaystyle\int_{1}^{3}(u^5-8u^4+22u^3-24u^2+9u)du\)
\(=\displaystyle\frac{π}{4^3\sqrt{2}}\left[\displaystyle\frac{u^6}{6}-\displaystyle\frac{8u^5}{5}+\displaystyle\frac{11u^4}{2}-8u^3+\displaystyle\frac{9u^2}{2}\right]_{1}^{3}\)
\(=\displaystyle\frac{π}{4^3\sqrt{2}}\left\{3^3(\displaystyle\frac{9}{2}-\displaystyle\frac{72}{5}+\displaystyle\frac{33}{2}-8+\displaystyle\frac{3}{2})-(\displaystyle\frac{1}{6}-\displaystyle\frac{8}{5}+\displaystyle\frac{11}{2}-8+\displaystyle\frac{9}{2})\right\}\)
\(=\displaystyle\frac{π}{4^3\sqrt{2}}(\displaystyle\frac{27}{10}-\displaystyle\frac{17}{30})\)
\(=\displaystyle\frac{π}{64\sqrt{2}}\cdot\displaystyle\frac{64}{30}\)
\(=\displaystyle\frac{\sqrt{2}}{60}π\)
(イ)の方法
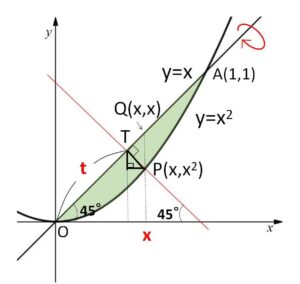
線分\(OA\ (=\sqrt{2})\) 上に点\(T\)をとり、\(OT=t\) (\(0≦t≦\sqrt{2}\)) とおく
図のように\(T\)を通る回転軸と垂直な直線と\(y=x^2\)の交点のうち\(0≦x≦1\)の部分にあるものを\(P\)とし、\(P(x,x^2)\) とおく。また点\(Q\)を\(Q(x,x)\)となるようにとる。
\(QP=x-x^2\) であり、\(45°\)の直角三角形の辺の比から
\(TP=\displaystyle\frac{1}{\sqrt{2}}(x-x^2)\)
(\(x,t\)の関係式を作ります)
\(OT+TQ=OQ\) より
\(t+\displaystyle\frac{1}{\sqrt{2}}(x-x^2)=\sqrt{2}x\)・・・②
②より
\(t=\displaystyle\frac{\sqrt{2}}{2}(x^2+x)\)・・・②’ だから
\(dt=\displaystyle\frac{\sqrt{2}}{2}(2x+1)dx\)
よって体積\(V\)は
\(V=\displaystyle\int_{0}^{\sqrt{2}}πTP^2dt\)
\(=π\displaystyle\int_{0}^{1}\displaystyle\frac{1}{2}(x-x^2)^2\cdot\displaystyle\frac{\sqrt{2}}{2}(2x+1)dx\)
\(=\displaystyle\frac{\sqrt{2}π}{4}\displaystyle\int_{0}^{1}x^2(1-x)^2(2x+1)dx\)
\(=\displaystyle\frac{\sqrt{2}π}{4}\displaystyle\int_{0}^{1}(2x^5-3x^4+x^2)dx\)
\(=\displaystyle\frac{\sqrt{2}π}{4}\left[\displaystyle\frac{x^6}{3}-\displaystyle\frac{3x^5}{5}+\displaystyle\frac{x^3}{3}\right]_{0}^{1}\)
\(=\displaystyle\frac{\sqrt{2}}{60}π\)
(解法2)全体を回転させる方法
回転は複素数を用いて、媒介変数表示の回転体に帰着させます。
全体を\(-45°\)回転させて、\(x\)軸に関する回転体の体積を求めればよい。
\(y=x^2\) 上に点\(P(t,t^2)\) をとる。\(y=x^2\) と \(y=x\) の交点の\(x\)座標は \(x=0,1\) なので、\(0≦t≦1\) とすればよい。
点\(P\)の回転後の座標を\(P'(x,y)\)とすると
\(x+yi=(t+t^2i)\{\cos(-45°)+i\sin(-45°)\}\)
\(x+yi=(t+t^2i)(\displaystyle\frac{1}{\sqrt{2}}-\displaystyle\frac{1}{\sqrt{2}}i)\)
\(x+yi=\displaystyle\frac{t^2+t}{\sqrt{2}}+\displaystyle\frac{t^2-t}{\sqrt{2}}i\)
よって \(y=x^2\) の回転後の曲線は、次のように表される。
\(x=\displaystyle\frac{t^2+t}{\sqrt{2}}\)
\(y=\displaystyle\frac{t^2-t}{\sqrt{2}}\)
(\(0≦t≦1\))
\(\displaystyle\frac{dx}{dt}=\displaystyle\frac{2t+1}{\sqrt{2}}>0\) (単調増加)
\(\displaystyle\frac{dy}{dt}=\displaystyle\frac{2t-1}{\sqrt{2}}\) (\(t=\displaystyle\frac{1}{2}\) で極小)
\(t=0,1\) のときそれぞれ \(x=0\),\(y=0\)、\(x=\sqrt{2}\),\(y=0\) なので、回転後のグラフは次のようになる。
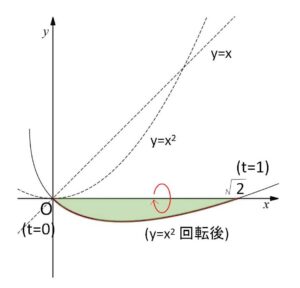
したがって体積\(V\)は
\(V=π\displaystyle\int_{0}^{\sqrt{2}}y^2dx\)
\(=π\displaystyle\int_{0}^{1}(\displaystyle\frac{t^2-t}{\sqrt{2}})^2\cdot\displaystyle\frac{2t+1}{\sqrt{2}}dt\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\displaystyle\int_{0}^{1}(t^2-t)^2(2t+1)dt\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\displaystyle\int_{0}^{1}(2t^5-3t^4+t^2)dt\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\left[\displaystyle\frac{t^6}{3}-\displaystyle\frac{3t^5}{5}+\displaystyle\frac{t^3}{3}\right]_{0}^{1}\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\cdot\displaystyle\frac{1}{15}\)
\(=\displaystyle\frac{\sqrt{2}}{60}π\)
(例題2)
\(y=x^2-3x\) と \(y=x\) とで囲まれた部分を、直線 \(y=x\) の周りに1回転してできる回転体の体積\(V\)を求めよ。
(解答1)半径を\(t\)で表し\(t\)で積分する方法
なお解答は省きますが、\(x\)で表して置換積分してももちろんよいです。
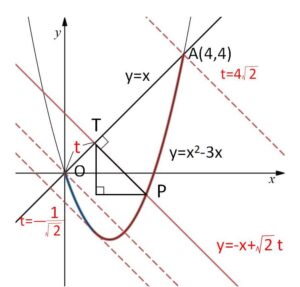
\(y=x\) と \(y=x^2-3x\) は、2点 \(O(0,0),A(4,4)\) で交わる。
\(O\)から\(A\)方向を正の向きとして\(t\)軸を設定し、座標\(t\)であるときの点を\(T(\displaystyle\frac{t}{\sqrt{2}},\displaystyle\frac{t}{\sqrt{2}})\) とおく。
\(T\)を通り \(y=x\) に垂直な直線の方程式は
\(y=-(x-\displaystyle\frac{t}{\sqrt{2}})+\displaystyle\frac{t}{\sqrt{2}}\)
整理すると
\(y=-x+\sqrt{2}t\)・・・①
①と \(y=x^2-3x\) より\(y\)を消去すると
\(x^2-3x=-x+\sqrt{2}t\)
\(x^2-2x-\sqrt{2}t=0\)
\(x=1±\sqrt{1+\sqrt{2}t}\)・・・②
回転軸に垂直な直線①と\(y=x^2-3x\)との交点のうち、\(0≦x≦4\)の部分にあるものを\(P\)とおくと②と \(OA=4\sqrt{2}\) より
\(t=-\displaystyle\frac{1}{\sqrt{2}}\) のとき接し、\(P\)は1個
\(-\displaystyle\frac{1}{\sqrt{2}}<t≦0\) のとき、\(P\)は2個
\(0<t≦4\sqrt{2}\) のとき、\(P\)は1個 (②の\(-\)の方が不適になる)
よって\(45°\)の直角三角形の辺の比から
\(TP=\sqrt{2}\left|1±\sqrt{1+\sqrt{2}t}-\displaystyle\frac{t}{\sqrt{2}}\right|\)
\(=\displaystyle\frac{\sqrt{2}}{2}\left|2-\sqrt{2}t±2\sqrt{1+\sqrt{2}t}\right|\)
(曲線を2分割して、2乗の差をとります)
したがって
\(V=π\displaystyle\int_{-\frac{1}{\sqrt{2}}}^{4\sqrt{2}}\displaystyle\frac{1}{2}(2-\sqrt{2}t+2\sqrt{1+\sqrt{2}t})^2dt-π\displaystyle\int_{-\frac{1}{\sqrt{2}}}^{0}\displaystyle\frac{1}{2}(2-\sqrt{2}t-2\sqrt{1+\sqrt{2}t})^2dt\)
\((=I_1-I_2\)) とおく。
(1次式の平方根は丸ごと置換が基本ですが、今回は中身を置換してみます)
\(I_1\)について
\(1+\sqrt{2}t=u\) とおくと
\(I_1=\displaystyle\frac{π}{2}\displaystyle\int_{0}^{9}(-u+3+2\sqrt{u})^2\cdot\displaystyle\frac{1}{\sqrt{2}}du\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\displaystyle\int_{0}^{9}\left\{(-u+3)^2+4(-u+3)\sqrt{u}+4u\right\}du\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\displaystyle\int_{0}^{9}\left\{(u-3)^2-4u^{\frac{3}{2}}+12u^{\frac{1}{2}}+4u\right\}du\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\left[\displaystyle\frac{(u-3)^3}{3}-\displaystyle\frac{8u^{\frac{5}{2}}}{5}+8u^{\frac{3}{2}}+2u^2\right]_{0}^{9}\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\left\{(6^2\cdot2-\displaystyle\frac{8\cdot3^5}{5}+8\cdot3^3+2\cdot9^2)-(-9)\right\}\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\left\{3^2\cdot2(4-\displaystyle\frac{4\cdot27}{5}+4\cdot3+9)-(-9)\right\}\)
\(=\displaystyle\frac{π}{2\sqrt{2}}(\displaystyle\frac{18\cdot17}{5}+9)\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\cdot\displaystyle\frac{351}{5}\)
\(I_2\)について
同様に \(1+\sqrt{2}t=u\) とおくと
\(I_2=\displaystyle\frac{π}{2}\displaystyle\int_{0}^{1}(-u+3-2\sqrt{u})^2\cdot\displaystyle\frac{1}{\sqrt{2}}du\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\displaystyle\int_{0}^{1}\left\{(u-3)^2+4u^{\frac{3}{2}}-12u^{\frac{1}{2}}+4u\right\}du\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\left[\displaystyle\frac{(u-3)^3}{3}+\displaystyle\frac{8u^{\frac{5}{2}}}{5}-8u^{\frac{3}{2}}+2u^2\right]_{0}^{1}\)
\(=\displaystyle\frac{π}{2\sqrt{2}}(\displaystyle\frac{-8}{3}+\displaystyle\frac{8}{5}-8+2+9)\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\cdot\displaystyle\frac{29}{15}\)
ゆえに
\(V=\displaystyle\frac{π}{2\sqrt{2}}(\displaystyle\frac{351}{5}-\displaystyle\frac{29}{15})\)
\(=\displaystyle\frac{π}{2\sqrt{2}}\cdot\displaystyle\frac{1024}{15}\)
\(=\displaystyle\frac{256\sqrt{2}}{15}π\)
(解答2)回転させる方法
全体を\(-45°\)回転させて\(x\)軸周りの回転体の体積を求めればよい。
\(y=x\) と \(y=x^2-3x\) の交点の\(x\)座標は、\(x=0,4\)
よって \(0≦t≦4\) として点\(P(t,t^2-3t)\) をとり、回転後の点を\(P'(x,y)\)とすると
\(x+yi=\{t+(t^2-3t)i\}(\displaystyle\frac{1}{\sqrt{2}}-\displaystyle\frac{1}{\sqrt{2}}i)\)
\(x+yi=\displaystyle\frac{t^2-2t}{\sqrt{2}}+\displaystyle\frac{t^2-4t}{\sqrt{2}}i\)
よって \(y=x^2-3x\) を回転させた曲線は次のように表される。
\(x=\displaystyle\frac{t^2-2t}{\sqrt{2}}\)
\(y=\displaystyle\frac{t^2-4t}{\sqrt{2}}\)
\((0≦t≦4)\)
\(\displaystyle\frac{dx}{dt}=\sqrt{2}(t-1)\) (\(t=1\)で折り返すことになる)
\(\displaystyle\frac{dy}{dt}=\sqrt{2}(t-2)\)
\(t=0\) のとき \((x,y)=(0,0)\)
\(t=1\) のとき \((x,y)=(-\displaystyle\frac{1}{\sqrt{2}},-\displaystyle\frac{3}{\sqrt{2}})\)
\(t=4\) のとき \((x,y)=(4\sqrt{2},0)\)
となるから、グラフは次の通り。
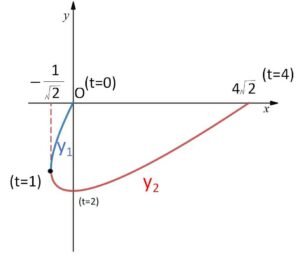
したがって
\(V=π\displaystyle\int_{-\frac{1}{\sqrt{2}}}^{4\sqrt{2}}y_2^2dx-π\displaystyle\int_{-\frac{1}{\sqrt{2}}}^{0}y_1^2dx\)
\(=π\displaystyle\int_{1}^{4}\displaystyle\frac{(t^2-4t)^2}{2}\cdot\sqrt{2}(t-1)dt-π\displaystyle\int_{1}^{0}\displaystyle\frac{(t^2-4t)^2}{2}\cdot\sqrt{2}(t-1)dt\)
\(=\displaystyle\frac{\sqrt{2}π}{2}\displaystyle\int_{0}^{4}(t^2-4t)^2(t-1)dt\)
\(=\displaystyle\frac{\sqrt{2}π}{2}\displaystyle\int_{0}^{4}(t^5-9t^4+24t^3-16t^2)dt\)
\(=\displaystyle\frac{\sqrt{2}π}{2}\left[\displaystyle\frac{t^6}{6}-\displaystyle\frac{9}{5}t^5+6t^4-\displaystyle\frac{16}{3}t^3\right]_{0}^{4}\)
\(=\displaystyle\frac{\sqrt{2}π}{2}\cdot4^4\cdot2\left(\displaystyle\frac{4}{3}-\displaystyle\frac{18}{5}+3-\displaystyle\frac{2}{3}\right)\)
\(=4^4\sqrt{2}π\cdot\displaystyle\frac{1}{15}\)
\(=\displaystyle\frac{256\sqrt{2}}{15}π\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→連立不等式と体積 back→x,y軸に平行な直線に関する回転体