対数関数のグラフと大小関係

対数関数のグラフについて考えていきます。

・対数関数のグラフ
真数を正の数\(x\)とする関数 \(y=\log_{2}x\)  のグラフについて

指数関数のグラフと同様に分かりやすい座標 \((x,y)\) をいくつか\(xy\)平面にプロットしてみてもよいですが、ここでは違った視点で対数関数のグラフを考えてみます。

\(y=\log_{2}x\)　\(⇔\)　\(x=2^y\)　(この2つは全く同じことを表している)

ですから、対数関数 \(y=\log_{2}x\)  は、指数関数 \(y=2^x\) のグラフの\((x,y)\)をちょうど入れ替えたものなります。では \(y=2^x\) のグラフの\((x,y)\)を入れ替えたものはどのような形状になるでしょうか。

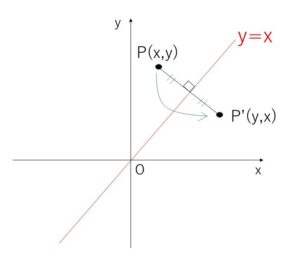
もとの点\(P\)\((x,y)\) と 移動後の点\(P’\)\((y,x)\) について

(1)\(P,P’\) の中点 \((\displaystyle\frac{x+y}{2},\displaystyle\frac{x+y}{2})\) は、\(x,y\)座標が同じ
(2)\(P,P’\) の傾きは、\(x≠y\) のとき、\(\displaystyle\frac{y-x}{x-y}=-1\)

となり、\(P,P’\)は 直線\(y=x\) について対称な点であることが分かります。(\(x=y\)でも同じ2点\(P,P’\)が \(y=x\)上にあるので成り立つ)

したがって、\(y=2^x\) の グラフを \(y=x\) について対称移動したものが \(x=2^y\) のグラフであり、それはすなわち \(y=\log_{2}x\) のグラフです。

そして、指数関数 \(y=a^x\) の形状は \(0<a<1\) と \(a>1\) の場合で異なるので、対数関数のグラフも同様にこの底の値で異なることになります。

以上のことから、
\(y=\log_{a}x\) (\(a\)は1でない正の数)
のグラフは次の通りです。

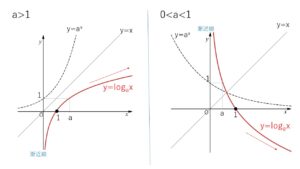
対数関数 \(y=\log_{a}x\) のグラフの特徴をまとめると

(1)
\(x\)は真数なので、定義域(\(x\)の範囲)は正の実数全体、
値域(\(y\)の範囲)は、指数関数でいうと指数の部分なので実数全体。(グラフから判断してもよい)

(2)
グラフは \(a\)の値にかかわず \((1,0)\) を通り、漸近線は \(y\)軸
(\(y=a^x\) が \((0,1)\)を通り、漸近線が\(x\)軸であることに対応)

(3)\(a>1\) のときは右上がりの曲線(単調増加関数)、\(0<a<1\) のときは右下がりの曲線(単調減少関数)

(4)
\(a>1\)　「\(x≧1\) のとき \(y≧0\),　\(0<x<1\) のとき \(y<0\)」
\(0<a<1\)   「\(x≧1\) のとき \(y≦0\),　\(0<x<1\) のとき \(y>0\)」

・対数の相等と大小
以下 \(a\)を1でない正の数、\(p,q>0\) とします。

対数関数も、指数関数と同様に1:1対応の関数なので

\(\log_{a}p=\log_{a}q\)　\(⇔\)　\(p=q\)　(対数の相等)

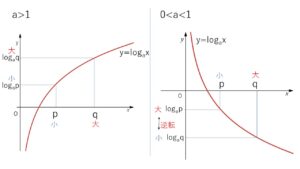
また、\(y=\log_{a}x\) について

\(a>1\) のときはグラフより「\(x\)の値が増加すると、\(y\)の値が増加」するので
\(0<p<q\)　\(⇔\)　\(\log_{a}p<\log_{a}q\)　(大小一致)

\(0<a<1\) のときはグラフより「\(x\)の値が増加すると、\(y\)の値が減少」するので
\(0<p<q\)　\(⇔\)　\(\log_{a}p>\log_{a}q\)　(大小逆転)

・指数関数のグラフの移動
指数関数、2次関数、ひいては一般の関数の場合と同様です。(割愛します)

(例題)
(1)\(a=7\), \(b=3\log_{2}5\), \(c=3+\log_{2}3+\log_{2}5\) とする。\(a,b,c\) の大小を比較せよ。

(2)\(\log_{0.5}4\), \(\log_{2}4\), \(\log_{3}4\) の大小を比較せよ。

(3)\(\log_{2}3\), \(\log_{3}4\), \(\log_{4}2\) の大小を比較せよ。

(解答)
(1)

\(a=7\)
\(=7\log_{2}2\)
\(=\log_{2}2^7\)
\(=\log_{2}128\)

\(b=3\log_{2}5\)
\(=\log_{2}5^3\)
\(=\log_{2}125\)

\(c=3+\log_{2}3+\log_{2}5\)
\(=\log_{2}2^3+\log_{2}3+\log_{2}5\)
\(=\log_{2}(2^3\cdot3\cdot5)\)
\(=\log_{2}120\)

底が2なので、真数の大小を比較して
\(a>b>c\)

(2)

\(\log_{0.5}4\)\(=\displaystyle\frac{1}{\log_{4}0.5}\)

\(\log_{2}4\)\(=\displaystyle\frac{1}{\log_{4}2}\)

\(\log_{3}4\)\(=\displaystyle\frac{1}{\log_{4}3}\)

ここで、\(\log_{4}0.5<0\) で
\(0<{\log_{4}2}<\log_{4}3\)　より
\(\displaystyle\frac{1}{\log_{4}2}>\displaystyle\frac{1}{\log_{4}3}\)

したがって
\(\log_{0.5}4<\log_{3}4<\log_{2}4\)

(3)

\(\log_{2}3>1\), \(\log_{3}4>1\), \(\log_{4}2<1\) より

1つ目と2つ目を比較すればよい。

(底を2にあわせると)
\(\log_{3}4=\displaystyle\frac{2}{\log_{2}3}\) より

\(\log_{2}3-\log_{3}4\)
\(=\log_{2}3-\displaystyle\frac{2}{\log_{2}3}\)
\(=\displaystyle\frac{(\log_{2}3)^2-2}{\log_{2}3}\)・・・①

ここで、\(1.5^2=2.25>2\) より
\(1.5>\sqrt{2}\) だから

\(\log_{2}3-\sqrt{2}\)
\(>\log_{2}3-1.5\)
\(=\log_{2}3-\log_{2}2^{1.5}\)
\(=\log_{2}3-\log_{2}\sqrt{8}\)
\(=\log_{2}\sqrt{9}-\log_{2}\sqrt{8}\)
\(>0\)

よって \(\log_{2}3>(1.5)>\sqrt{2}\) であり
①の分母分子ともに正なので

\(\log_{2}3>\log_{3}4\)

したがって
\(\log_{2}3>\log_{3}4>\log_{4}2\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→対数方程式　back→対数と指数