対数関数の文章問題への利用

対数を利用する文章問題について見ていきます。

(例題)
ある培養液中の細菌が、\(T\)分間で細菌数が\(2\)倍に増殖するとする。また、1回のろ過により細菌数は\(d％\)減少するものとする。ただし、ろ過にかかる時間は無視できるものとする。

(1)いま、その培養液中に\(N\)個の細菌が存在するとする。\(t\)分後の細菌の個数\(n\)を求めよ。
(2)\(c\)時間後に何回か培養液のろ過をする。培養開始時点よりも細菌数を少なくするために必要な最小のろ過回数を\(f\)とする。必要ならば、記号\([\) \(]\)を用いて、\(c,d\)から\(f\)を求める式を書け。ただし、\([x]\)は\(x\)を超えない最大の整数を表す。
(2) (2)において、\(N=2\), \(T=20\), \(d=75\) とする。このとき、\(1≦c≦3\) における\(c\) と \(f\) の関係をグラフで示せ。

(解答)
(1)

\(T\)分間で\(2\)倍に増殖というのは、\(T\)分ごと(\(T\)分あたり)に\(2\)倍になるということです。よって具体的に考えると次の通りです。
\(T\)分後→\(2\)倍
\(2T\)分後→\(2×2\)倍
\(3T\)分後→\(2×2×2\)倍　(\(6\)倍ではない)

細菌数は\(T\)分間で\(2\)倍になるので、\(t\)分間では、\(2^{\frac{t}{T}}\) 倍になる。

したがって、初期の細菌数は\(N\)だから
\(n=N×2^{\frac{t}{T}}\)

(2)

\(c\)時間後には細菌数はいくらか増加しています。ろ過することで細菌数が減りますが、初期の細菌数より少なくするためには最低何回ろ過する必要があるかというのがこの設問の意味です。
1回のろ過で \(d％\) 減るので、1回のろ過で細菌数は \(1-\displaystyle\frac{d}{100}\) 倍になります。

\(c\) 時間後の細菌数は(1)より
\(N×2^{\frac{60c}{T}}\)

\(f\) 回ろ過した後の細菌数は
\(N×2^{\frac{60c}{T}}×(1-\displaystyle\frac{d}{100})^{f}\)

これが初期の細菌数 \(N\) より小さくなるので
\(N>N×2^{\frac{60c}{T}}×(1-\displaystyle\frac{d}{100})^{f}\)・・・①

回数\(f\)が知りたいので、①を\(f\)について解きます。
\(f\)は指数のところにあるため、対数をとることになります。なお解答では常用対数をとりますが、底はなんでもよいです。

①の両辺を \(N(>0)\) で割って

\(1>2^{\frac{60c}{T}}×(1-\displaystyle\frac{d}{100})^{f}\)

常用対数をとって
\(0>\displaystyle\frac{60c}{T}\log_{10}2+f\log_{10}(1-\displaystyle\frac{d}{100})\)

\(0<1-\displaystyle\frac{d}{100}<1\) より
\(\log_{10}(1-\displaystyle\frac{d}{100})\color{red}{<0}\) だから

\(f>-\displaystyle\frac{\displaystyle\frac{60c}{T}\log_{10}2}{\log_{10}(1-\displaystyle\frac{d}{100})}\)・・・②

実際に作業することをイメージすれば分かりますが、ろ過する回数\(f\)は自然数です。
ここで②の右辺は正の数ですが、自然数であるとは限らないのでガウス記号\([\)　\(]\)を使うことになります。例えば \(f>5.5\) の場合、最小の\(f\)は\(f=5+1=[5.5]+1\) となるので、これを文字式についても同じように考えます。右辺が整数値でも不等号にイコールが入っていないので同様に、ガウス記号をとって\(1\)を足すことになります。

したがって最小のろ過回数は

\(f=[-\displaystyle\frac{60c}{T}\cdot\displaystyle\frac{\log_{10}2}{\log_{10}(1-\displaystyle\frac{d}{100})}]+1\)

(3)

(2)で求めた\(f\)に具体的に代入するだけです。なお、\(f\)の式に\(N\)が出てこないので、\(N=2\) は使いません。(\(N\)が出てこないということは初期細胞数は、ろ過回数に関係ないということです)

(2)で求めた\(f\)に、 \(T=20\), \(d=75\) を代入して

\(f=[-\displaystyle\frac{60c}{20}\cdot\displaystyle\frac{\log_{10}2}{\log_{10}(1-\displaystyle\frac{75}{100})}]+1\)

\(=[-3c\cdot\displaystyle\frac{\log_{10}2}{\log_{10}\displaystyle\frac{1}{4}}]+1\)

\(=[\displaystyle\frac{3}{2}c]+1\)

ガウス記号の中身が整数値になるときにグラフは変化します。
\(1≦c≦3\) より、\(\displaystyle\frac{3}{2}≦\displaystyle\frac{3}{2}c≦\displaystyle\frac{9}{2}\) だから
\(\displaystyle\frac{3}{2}c=2,3,4\)
つまり、\(c=\displaystyle\frac{4}{3},2,\displaystyle\frac{8}{3}\) が境目です。

(ア)\(1≦c<\displaystyle\frac{4}{3}\) のとき
\(f=1+1=2\)

(イ)\(\displaystyle\frac{4}{3}≦c<2\) のとき
\(f=2+1=3\)

(ウ)\(2≦c<\displaystyle\frac{8}{3}\) のとき
\(f=3+1=4\)

(エ)\(\displaystyle\frac{8}{3}≦c≦3\) のとき
\(f=4+1=5\)

以上よりグラフは次の通り。

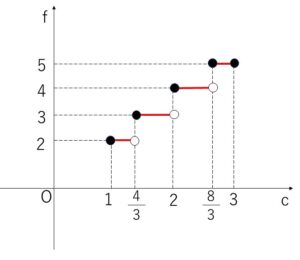
対数　文章問題　グラフ

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→最高位の数と個数