集合の基礎②(共通部分・和集合)

前回に引き続き集合の基礎知識について学びます。

・共通部分と和集合
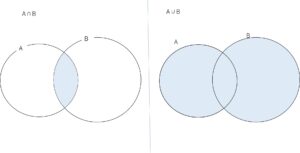
2つの集合\(A,B\)について、\(A,B\)のどちらにも属する要素全体の集合を、\(A\)と\(B\)の共通部分といい、\(A \cap B\)　と表します。また、\(A,B\)の少なくとも一方に属する要素全体の集合を、\(A\)と\(B\)の和集合といい、\(A \cup B\) と表します。つまり

\(A \cap B=\{x|x\in A\)　かつ　\(x\in B\}\)
\(A \cup B=\{x|x\in A\)　または　\(x\in B\}\)

となります。ベン図で表すと次の通りです。

和集合共通部分1

次の具体例で考えると分かりやすいと思います。

(例)
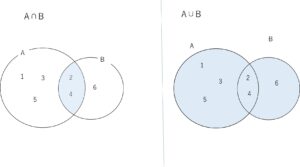
\(A=\{1,2,3,4,5\}\)　\(B=\{2,4,6\}\) のとき

\(A \cap B=\{2,4\}\),　\(A \cup B=\{1,2,3,4,5,6\}\)

\(A \cap B\)の要素は両方に属する要素なので2と4、\(A \cup B\)の要素は\(A,B\)どちらか一方に属していればよいので1,2,3,4,5,6となります。\(\cap\)は「かつ」、\(\cup\)は「または」と考えると分かりやすいと思います。

・空集合
例えば2つの集合、\(A=\{1,2\}\), \(B=\{3,4,7\}\)を考えると、2つの集合には共通の要素がありません。つまり\(A \cap B\)は要素をもたない集合です。要素をもたない集合を空集合(くうしゅうごう)といい、\(φ\)(ファイ) で表します。(\(A \cap B=φ\))　なお、どんな集合\(A\)についても空集合は\(A\)の部分集合であるとします。

\(A\)の一部には何もない集合があると考えます。
要素が何もない集合である空集合は数字でいうと\(0\)に対応するものです。ただし集合\(\{0\}\)は\(0\)という要素があるので空集合ではないことに注意してください。

少し問題を解いてみます。

(問題1)
\(U\)を整数全体の集合とするとき、集合
\(A=\{x|x\in U,-2≦x<2\}\),　\(B=\{x|x\in U,x^2+6x+5<0\}\)
について、\(A \cap B\),　\(A \cup B\)　を要素を書き並べて表せ。

\(A,B\)の要素を具体的に列挙して考えます。

(解答)
\(B\) について、\(x^2+6x+5<0\)　より　\((x+5)(x+1)<0\)　だから
\(-5<x<-1\) 　したがって\(A,B\)の要素を書き並べると
\(A=\{-2,-1,0,1\}\),　\(B=\{-4,-3,-2\}\)
よって
\(A \cap B=\{-2\}\)
\(A \cup B=\{-4,-3,-2,-1,0,1\}\)

(問題2)
2つの集合 \(A=\{x|2x^2-x-1>0\}\), \(B=\{x|x^2+2x<0\}\)　において、\(A \cap B\),\(A \cup B\)　を求めよ。

今度は具体的に要素を列挙することはできないので、\(x\)の範囲で考えます。

(解答)
\(A\)について、\(2x^2-x-1>0\)　より　\((2x+1)(x-1)>0\) だから
\(x<-\displaystyle\frac{1}{2}\)　または　\(x>1\)・・・①
\(B\)について、\(x^2+2x<0\)　より　\(x(x+2)<0\)　だから
\(-2<x<0\)・・・②

①かつ②の範囲を求めることにより
\(A \cap B=\{x|-2<x<-\displaystyle\frac{1}{2}\}\)

①または②の範囲を求めることにより
\(A \cup B=\{x|x<0,x>1\}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→集合の基礎③　back→集合の基礎①